Definizione - Funzione di trasferimento
La funzione di trasferimento di un sistema è una funzione nel dominio delle frequenze che ne descrive il comportamento, mettendo in relazione ingressi e uscite (nel dominio delle frequenze).
Considerando un ingresso \( \underline{X}(\omega)\) e un'uscita \( \underline{Y}(\omega)\), si ha che vale \[ \underline{Y}(\omega) = \underline{H}(\omega) \cdot \underline{X}(\omega) \] dove \( \underline{H}(\omega)\) è la funzione di trasferimento. Da ciò è possibile definire \[ \underline{H}(\omega) = \frac{\underline{Y}(\omega)}{\underline{X}(\omega)} \]
Considerando un ingresso \( \underline{X}(\omega)\) e un'uscita \( \underline{Y}(\omega)\), si ha che vale \[ \underline{Y}(\omega) = \underline{H}(\omega) \cdot \underline{X}(\omega) \] dove \( \underline{H}(\omega)\) è la funzione di trasferimento. Da ciò è possibile definire \[ \underline{H}(\omega) = \frac{\underline{Y}(\omega)}{\underline{X}(\omega)} \]
Definizione - Filtro
Un filtro è una rete che altera un segnale in base alla sua frequenza (altera quindi la risposta in frequenza).
Ogni filtro può essere descritto da una funzione di trasferimento \( \underline{H}(\omega)\) che ne descrive il comportamento.
Ogni filtro può essere descritto da una funzione di trasferimento \( \underline{H}(\omega)\) che ne descrive il comportamento.
Frequenza di taglio
La frequenza di taglio è un parametro di definizione delle proprietà di un filtro: tipicamente la si identifica come la frequenza in cui il modulo della funzione di trasferimento \( \left| \underline{H}(\omega) \right|\) è uguale a \( \; {}^{1} /_{\sqrt{2}\;}\) (ovvero circa \( 0.707\)).Definizione - Filtro passa-basso
Un filtro passa-basso ideale è una rete caratterizzata dalla seguente funzione di trasferimento 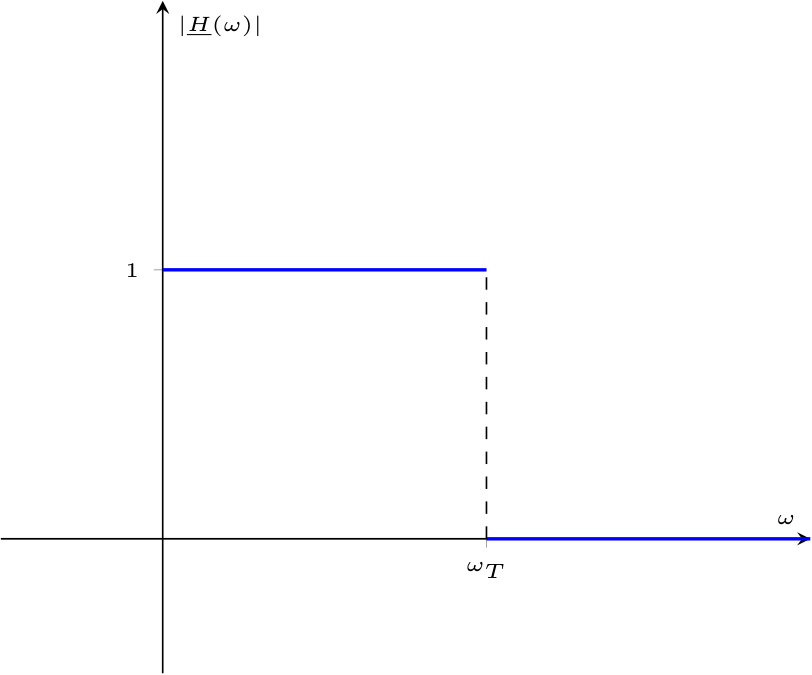 dove \( \omega_T\) è la pulsazione di taglio.
dove \( \omega_T\) è la pulsazione di taglio.
Questo filtro permette il passaggio di segnale ad una frequenza "bassa" mentre attenua i segnali ad una frequenza "alta" (rispetto alla frequenza di taglio). che, applicando Steinmetz, equivalerebbe al seguente circuito
che, applicando Steinmetz, equivalerebbe al seguente circuito  in cui si considera come segnale di ingresso quello del generatore \( \underline{E}\) e come segnale in uscita la tensione ai capi del condensatore \( \underline{V}_C\).
in cui si considera come segnale di ingresso quello del generatore \( \underline{E}\) e come segnale in uscita la tensione ai capi del condensatore \( \underline{V}_C\).
Calcolando \( \underline{V}_C\), considerando la formula del partitore di tensione, si ha che \[ \begin{array}{ccl} \underline{V}_C & = & \underline{E} \cdot \frac{\underline{Z}_C}{\underline{Z}_R + \underline{Z}_C} \\ & = & \underline{E} \cdot \frac{\frac{1}{\jmath \cdot \omega \cdot C}}{R + \frac{1}{\jmath \cdot \omega \cdot C}} \\ & = & \underline{E} \cdot \frac{\frac{1}{\jmath \cdot \omega \cdot C}}{\frac{\jmath \cdot \omega \cdot C \cdot R + 1}{\jmath \cdot \omega \cdot C}} \\ & = & \underline{E} \cdot \frac{1}{\jmath \cdot \omega \cdot C \cdot R + 1} \end{array} \] da cui è poi possibile calcolare la funzione di trasferimento come \[ \begin{array}{ccl} \underline{H}(\omega) & = & \frac{\underline{V}_C}{\underline{E}} \\ & = & \frac{\underline{E} \cdot \frac{1}{\jmath \cdot \omega \cdot C \cdot R + 1}}{\underline{E}} \\ & = & \frac{1}{\jmath \cdot \omega \cdot C \cdot R + 1} \\ & \overset{\cdot \frac{1 - \jmath \cdot \omega \cdot C \cdot R}{1 - \jmath \cdot \omega \cdot C \cdot R}}{=} & \frac{1}{\jmath \cdot \omega \cdot C \cdot R + 1} \cdot \frac{1 - \jmath \cdot \omega \cdot C \cdot R}{1 - \jmath \cdot \omega \cdot C \cdot R} \\ & = & \frac{1 - \jmath \cdot \omega \cdot C \cdot R}{\omega^2 \cdot C^2 \cdot R^2 + 1} \end{array} \] È quindi possibile calcolare il modulo della funzione di trasferimento come \[ \begin{array}{ccl} \left| \underline{H}(\omega) \right| & = & \left| \frac{1}{1 + \jmath \cdot \omega \cdot C \cdot R} \right| \\ & = & \frac{1}{\sqrt{1 + \omega^2 \cdot C^2 \cdot R^2}} \end{array} \] da cui è possibile calcolare la pulsazione di taglio cercando il valore per cui il modulo è uguale a \( \; {}^{1} /_{\sqrt{2}\;}\) \begin{aligned} & \left| \underline{H}(\omega) \right| = \frac{1}{\sqrt{2}} & \iff \\ & \frac{1}{\sqrt{1 + \omega^2 \cdot C^2 \cdot R^2}} = \frac{1}{\sqrt{2}} & \iff \\ & 1 + \omega^2 \cdot C^2 \cdot R^2 = 2 & \iff \\ & \omega^2 = \frac{1}{R^2 \cdot C^2} & \iff \\ & \omega_T = \frac{1}{R \cdot C} & \end{aligned} Graficando tale relazione, si ottiene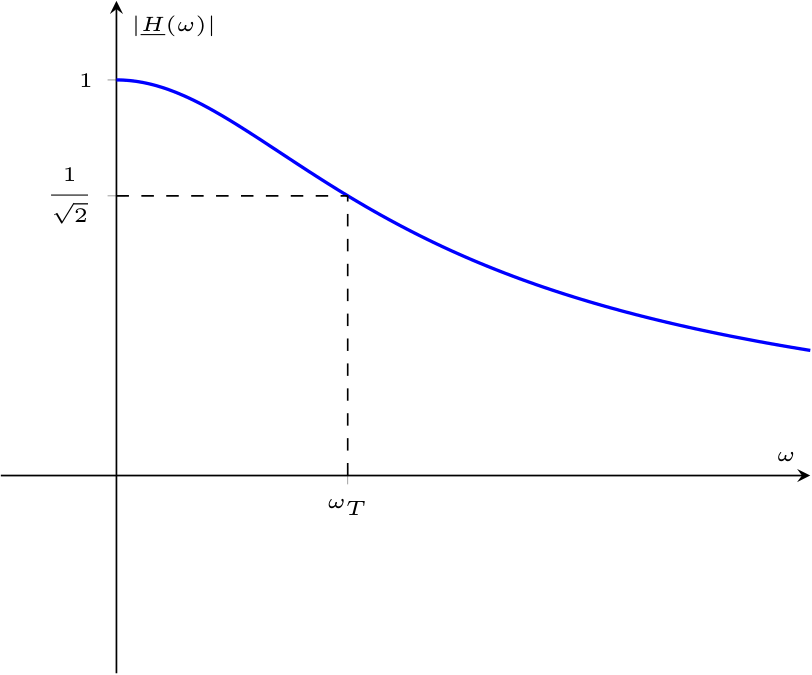 che approssima bene la funzione di trasferimento di un filtro passa-basso ideale.
che approssima bene la funzione di trasferimento di un filtro passa-basso ideale.
Considerando la fase, essa è uguale a \[ \begin{array}{ccl} \angle \underline{H}(\omega) & = & \arctan\left( \frac{\frac{-\omega \cdot C \cdot R}{\omega^2 \cdot C^2 \cdot R^2 + 1}}{\frac{1}{\omega^2 \cdot C^2 \cdot R^2 + 1}}\right) \\ & = & \arctan\left(\frac{-\omega \cdot C \cdot R}{1} \right) \\ & = & \arctan\left(-\omega \cdot C \cdot R \right) \end{array} \] che graficata è uguale a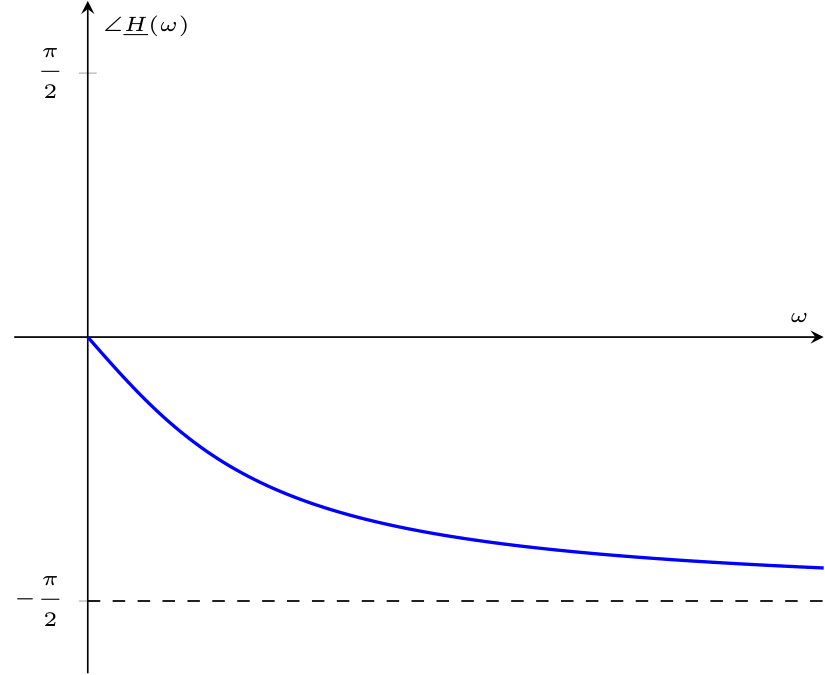

Questo filtro permette il passaggio di segnale ad una frequenza "bassa" mentre attenua i segnali ad una frequenza "alta" (rispetto alla frequenza di taglio).
Realizzazione di un filtro passa-basso con un circuito RC
È possibile realizzare un filtro passa-basso per la tensione utilizzando un circuito RC

Calcolando \( \underline{V}_C\), considerando la formula del partitore di tensione, si ha che \[ \begin{array}{ccl} \underline{V}_C & = & \underline{E} \cdot \frac{\underline{Z}_C}{\underline{Z}_R + \underline{Z}_C} \\ & = & \underline{E} \cdot \frac{\frac{1}{\jmath \cdot \omega \cdot C}}{R + \frac{1}{\jmath \cdot \omega \cdot C}} \\ & = & \underline{E} \cdot \frac{\frac{1}{\jmath \cdot \omega \cdot C}}{\frac{\jmath \cdot \omega \cdot C \cdot R + 1}{\jmath \cdot \omega \cdot C}} \\ & = & \underline{E} \cdot \frac{1}{\jmath \cdot \omega \cdot C \cdot R + 1} \end{array} \] da cui è poi possibile calcolare la funzione di trasferimento come \[ \begin{array}{ccl} \underline{H}(\omega) & = & \frac{\underline{V}_C}{\underline{E}} \\ & = & \frac{\underline{E} \cdot \frac{1}{\jmath \cdot \omega \cdot C \cdot R + 1}}{\underline{E}} \\ & = & \frac{1}{\jmath \cdot \omega \cdot C \cdot R + 1} \\ & \overset{\cdot \frac{1 - \jmath \cdot \omega \cdot C \cdot R}{1 - \jmath \cdot \omega \cdot C \cdot R}}{=} & \frac{1}{\jmath \cdot \omega \cdot C \cdot R + 1} \cdot \frac{1 - \jmath \cdot \omega \cdot C \cdot R}{1 - \jmath \cdot \omega \cdot C \cdot R} \\ & = & \frac{1 - \jmath \cdot \omega \cdot C \cdot R}{\omega^2 \cdot C^2 \cdot R^2 + 1} \end{array} \] È quindi possibile calcolare il modulo della funzione di trasferimento come \[ \begin{array}{ccl} \left| \underline{H}(\omega) \right| & = & \left| \frac{1}{1 + \jmath \cdot \omega \cdot C \cdot R} \right| \\ & = & \frac{1}{\sqrt{1 + \omega^2 \cdot C^2 \cdot R^2}} \end{array} \] da cui è possibile calcolare la pulsazione di taglio cercando il valore per cui il modulo è uguale a \( \; {}^{1} /_{\sqrt{2}\;}\) \begin{aligned} & \left| \underline{H}(\omega) \right| = \frac{1}{\sqrt{2}} & \iff \\ & \frac{1}{\sqrt{1 + \omega^2 \cdot C^2 \cdot R^2}} = \frac{1}{\sqrt{2}} & \iff \\ & 1 + \omega^2 \cdot C^2 \cdot R^2 = 2 & \iff \\ & \omega^2 = \frac{1}{R^2 \cdot C^2} & \iff \\ & \omega_T = \frac{1}{R \cdot C} & \end{aligned} Graficando tale relazione, si ottiene

Considerando la fase, essa è uguale a \[ \begin{array}{ccl} \angle \underline{H}(\omega) & = & \arctan\left( \frac{\frac{-\omega \cdot C \cdot R}{\omega^2 \cdot C^2 \cdot R^2 + 1}}{\frac{1}{\omega^2 \cdot C^2 \cdot R^2 + 1}}\right) \\ & = & \arctan\left(\frac{-\omega \cdot C \cdot R}{1} \right) \\ & = & \arctan\left(-\omega \cdot C \cdot R \right) \end{array} \] che graficata è uguale a

Nota bene - Circuito RC come filtro passa-alto
Considerando come uscita la tensione \( \underline{V}_R\), si ha che è possibile utilizzare questo circuito come filtro passa-alto.
Definizione - Filtro passa-alto
Un filtro passa-alto ideale è una rete caratterizzata dalla seguente funzione di trasferimento 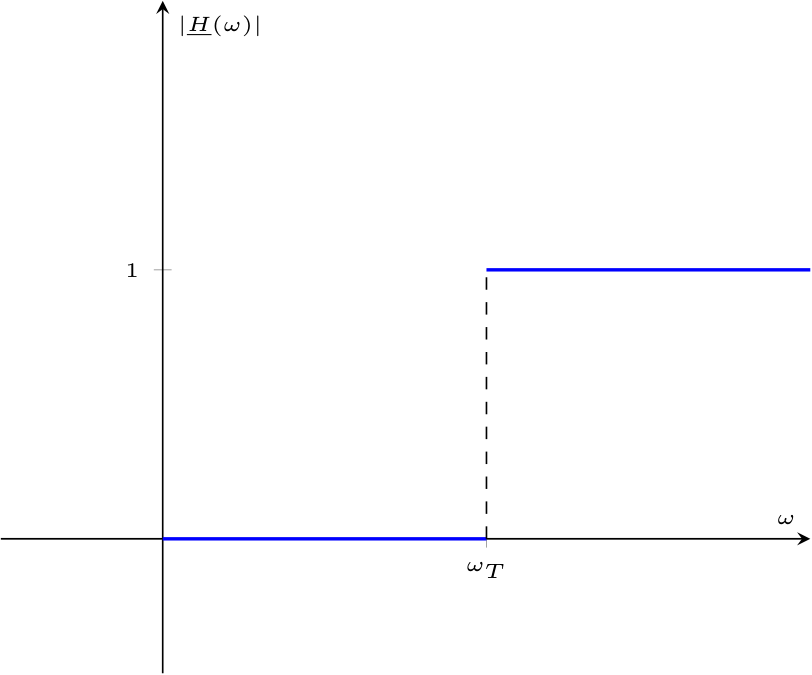 dove \( \omega_T\) è la pulsazione di taglio.
dove \( \omega_T\) è la pulsazione di taglio.
Questo filtro permette il passaggio di segnale ad una frequenza "alta" mentre attenua i segnali ad una frequenza "bassa" (rispetto alla frequenza di taglio). che, applicando Steinmetz, equivalerebbe al seguente circuito
che, applicando Steinmetz, equivalerebbe al seguente circuito 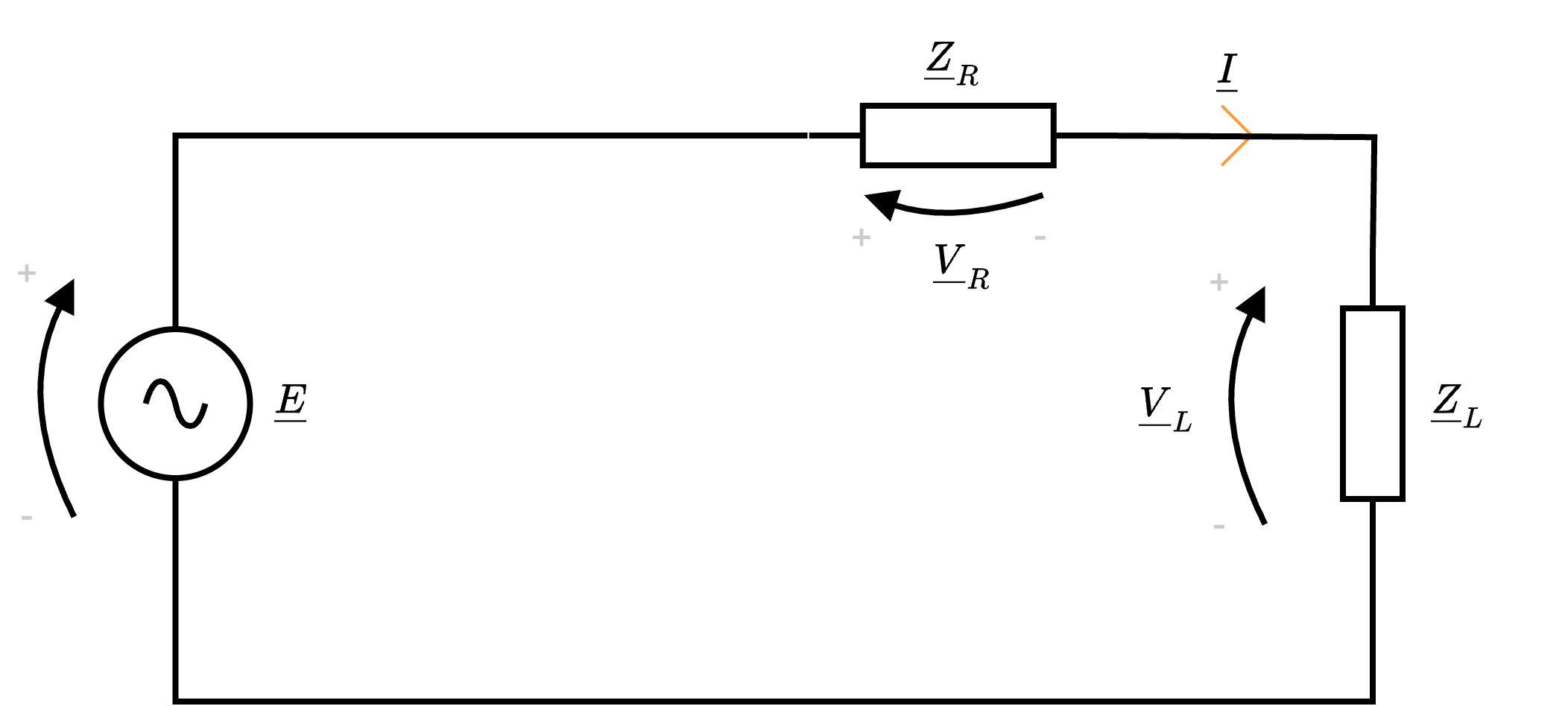 in cui si considera come segnale di ingresso quello del generatore \( \underline{E}\) e come segnale in uscita la tensione ai capi dell'induttore \( \underline{V}_L\).
in cui si considera come segnale di ingresso quello del generatore \( \underline{E}\) e come segnale in uscita la tensione ai capi dell'induttore \( \underline{V}_L\).
Calcolando \( \underline{V}_L\), considerando la formula del partitore di tensione, si ha che \[ \begin{array}{ccl} \underline{V}_L & = & \underline{E} \cdot \frac{\underline{Z}_L}{\underline{Z}_R + \underline{Z}_L} \\ & = & \underline{E} \cdot \frac{\jmath \cdot \omega \cdot L}{R + \jmath \cdot \omega \cdot L} \end{array} \] è poi possibile calcolare la funzione di trasferimento come \[ \begin{array}{ccl} \underline{H}(\omega) & = & \frac{\underline{V}_L}{\underline{E}} \\ & = & \frac{\underline{E} \cdot \frac{\jmath \cdot \omega \cdot L}{R + \jmath \cdot \omega \cdot L}}{\underline{E}} \\ & = & \frac{\jmath \cdot \omega \cdot L}{R + \jmath \cdot \omega \cdot L} \\ & \overset{\cdot \frac{\frac{1}{R}}{\frac{1}{R}}}{=} & \frac{\jmath \cdot \omega \cdot L}{R + \jmath \cdot \omega \cdot L} \cdot \frac{\frac{1}{R}}{\frac{1}{R}} \\ & = & \frac{\jmath \cdot \omega \cdot \frac{L}{R}}{1 + \jmath \cdot \omega \cdot \frac{L}{R}} \end{array} \] È quindi possibile calcolare il modulo della funzione di trasferimento come \[ \begin{array}{ccl} \left| \underline{H}(\omega) \right| & = & \left| \frac{\jmath \cdot \omega \cdot \frac{L}{R}}{1 + \jmath \cdot \omega \cdot \frac{L}{R}} \right| \\ & = & \frac{\omega \cdot \frac{L}{R}}{\sqrt{1 + \omega^2 \cdot \frac{L^2}{R^2}}} \end{array} \] da cui è possibile calcolare la pulsazione di taglio cercando il valore per cui il modulo è uguale a \( \; {}^{1} /_{\sqrt{2}\;}\) \begin{aligned} & \left| \underline{H}(\omega) \right| = \frac{1}{\sqrt{2}} & \iff \\ & \frac{\omega \cdot \frac{L}{R}}{\sqrt{1 + \omega^2 \cdot \frac{L^2}{R^2}}} = \frac{1}{\sqrt{2}} & \iff \\ & \omega_T = \frac{R}{L} & \end{aligned} Graficando tale relazione, si ottiene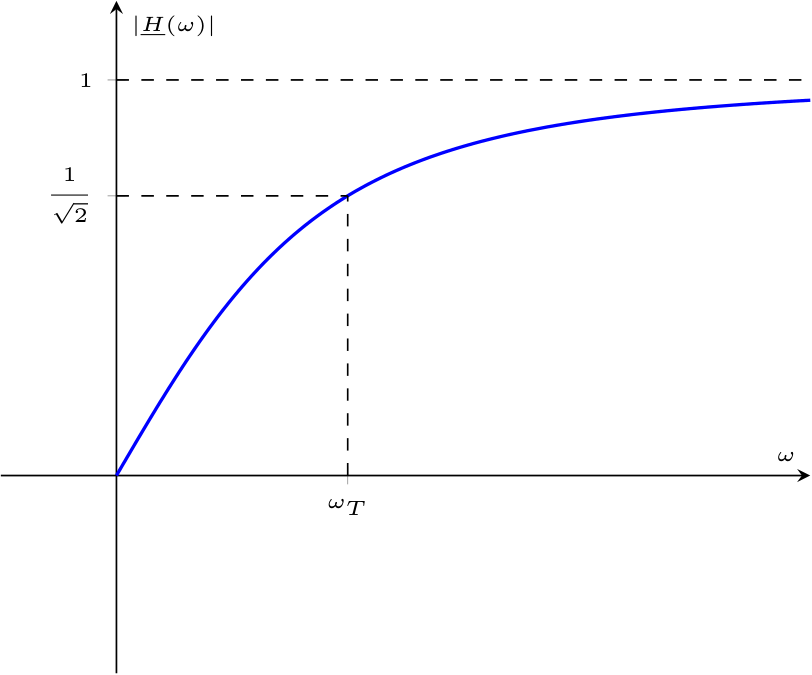 che approssima bene la funzione di trasferimento di un filtro passa-alto ideale.
che approssima bene la funzione di trasferimento di un filtro passa-alto ideale.
Al fine di calcolare la fase, consideriamo che la funzione di trasferimento \( \underline{H}(\omega)\) può essere scritta come \[ \begin{array}{ccl} \underline{H}(\omega) & = & \frac{\jmath \cdot \omega \cdot \frac{L}{R}}{1 + \jmath \cdot \omega \cdot \frac{L}{R}} \\ & \overset{\omega_T = \frac{R}{L}}{=} & \frac{\jmath \cdot \frac{\omega}{\omega_T}}{1 + \jmath \cdot \frac{\omega}{\omega_T}} \\ & \overset{\cdot \frac{1 - \jmath \cdot \frac{\omega}{\omega_T}}{1 - \jmath \cdot \frac{\omega}{\omega_T}}}{=} & \frac{\jmath \cdot \frac{\omega}{\omega_T}}{1 + \jmath \cdot \frac{\omega}{\omega_T}} \cdot \frac{1 - \jmath \cdot \frac{\omega}{\omega_T}}{1 - \jmath \cdot \frac{\omega}{\omega_T}} \\ & = & \frac{\jmath \cdot \frac{\omega}{\omega_T} + \frac{\omega^2}{(\omega_T)^2}}{1 + \frac{\omega^2}{(\omega_T)^2}} \end{array} \] da cui è possibile calcolare la fase \[ \begin{array}{ccl} \angle \underline{H}(\omega) & = & \arctan\left( \frac{\frac{\frac{\omega}{\omega_T}}{1 + \frac{\omega^2}{(\omega_T)^2}}}{\frac{\frac{\omega^2}{(\omega_T)^2}}{1 + \frac{\omega^2}{(\omega_T)^2}}} \right) \\ & = & \arctan\left( \frac{\frac{\omega}{\omega_T}}{\frac{\omega^2}{(\omega_T)^2}} \right) \\ & = & \arctan\left( \frac{1}{\frac{\omega}{\omega_T}} \right) \\ & = & \arctan\left( \frac{\omega_T}{\omega} \right) \\ & \overset{\frac{R}{L} = \omega_T}{=} & \arctan\left( \frac{\frac{R}{L}}{\omega} \right) \\ & = & \arctan\left( \frac{R}{L \cdot \omega} \right) \end{array} \] che graficata è uguale a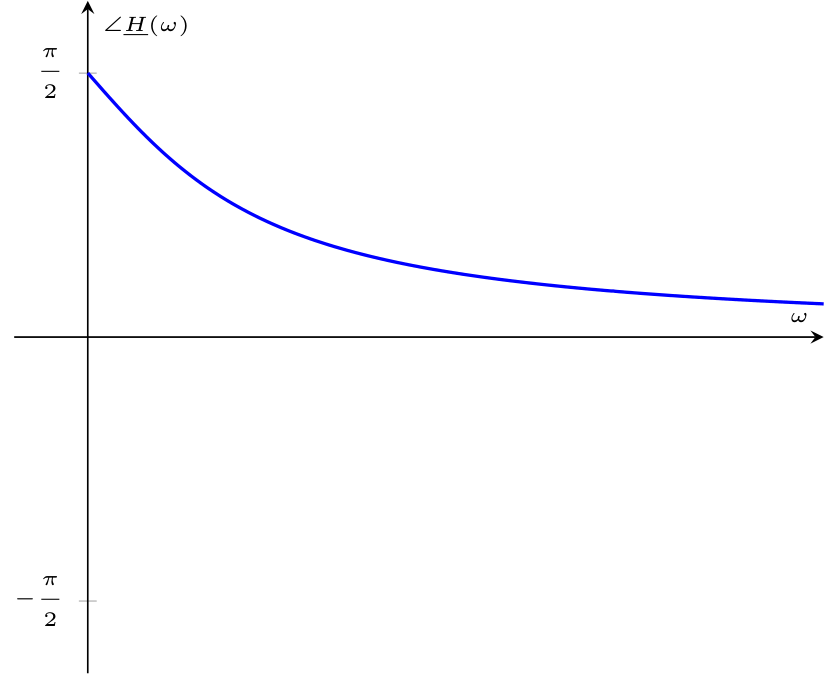

Questo filtro permette il passaggio di segnale ad una frequenza "alta" mentre attenua i segnali ad una frequenza "bassa" (rispetto alla frequenza di taglio).
Realizzazione di un filtro passa-alto con un circuito RL
È possibile realizzare un filtro passa-alto per la tensione utilizzando un circuito RL

Calcolando \( \underline{V}_L\), considerando la formula del partitore di tensione, si ha che \[ \begin{array}{ccl} \underline{V}_L & = & \underline{E} \cdot \frac{\underline{Z}_L}{\underline{Z}_R + \underline{Z}_L} \\ & = & \underline{E} \cdot \frac{\jmath \cdot \omega \cdot L}{R + \jmath \cdot \omega \cdot L} \end{array} \] è poi possibile calcolare la funzione di trasferimento come \[ \begin{array}{ccl} \underline{H}(\omega) & = & \frac{\underline{V}_L}{\underline{E}} \\ & = & \frac{\underline{E} \cdot \frac{\jmath \cdot \omega \cdot L}{R + \jmath \cdot \omega \cdot L}}{\underline{E}} \\ & = & \frac{\jmath \cdot \omega \cdot L}{R + \jmath \cdot \omega \cdot L} \\ & \overset{\cdot \frac{\frac{1}{R}}{\frac{1}{R}}}{=} & \frac{\jmath \cdot \omega \cdot L}{R + \jmath \cdot \omega \cdot L} \cdot \frac{\frac{1}{R}}{\frac{1}{R}} \\ & = & \frac{\jmath \cdot \omega \cdot \frac{L}{R}}{1 + \jmath \cdot \omega \cdot \frac{L}{R}} \end{array} \] È quindi possibile calcolare il modulo della funzione di trasferimento come \[ \begin{array}{ccl} \left| \underline{H}(\omega) \right| & = & \left| \frac{\jmath \cdot \omega \cdot \frac{L}{R}}{1 + \jmath \cdot \omega \cdot \frac{L}{R}} \right| \\ & = & \frac{\omega \cdot \frac{L}{R}}{\sqrt{1 + \omega^2 \cdot \frac{L^2}{R^2}}} \end{array} \] da cui è possibile calcolare la pulsazione di taglio cercando il valore per cui il modulo è uguale a \( \; {}^{1} /_{\sqrt{2}\;}\) \begin{aligned} & \left| \underline{H}(\omega) \right| = \frac{1}{\sqrt{2}} & \iff \\ & \frac{\omega \cdot \frac{L}{R}}{\sqrt{1 + \omega^2 \cdot \frac{L^2}{R^2}}} = \frac{1}{\sqrt{2}} & \iff \\ & \omega_T = \frac{R}{L} & \end{aligned} Graficando tale relazione, si ottiene

Al fine di calcolare la fase, consideriamo che la funzione di trasferimento \( \underline{H}(\omega)\) può essere scritta come \[ \begin{array}{ccl} \underline{H}(\omega) & = & \frac{\jmath \cdot \omega \cdot \frac{L}{R}}{1 + \jmath \cdot \omega \cdot \frac{L}{R}} \\ & \overset{\omega_T = \frac{R}{L}}{=} & \frac{\jmath \cdot \frac{\omega}{\omega_T}}{1 + \jmath \cdot \frac{\omega}{\omega_T}} \\ & \overset{\cdot \frac{1 - \jmath \cdot \frac{\omega}{\omega_T}}{1 - \jmath \cdot \frac{\omega}{\omega_T}}}{=} & \frac{\jmath \cdot \frac{\omega}{\omega_T}}{1 + \jmath \cdot \frac{\omega}{\omega_T}} \cdot \frac{1 - \jmath \cdot \frac{\omega}{\omega_T}}{1 - \jmath \cdot \frac{\omega}{\omega_T}} \\ & = & \frac{\jmath \cdot \frac{\omega}{\omega_T} + \frac{\omega^2}{(\omega_T)^2}}{1 + \frac{\omega^2}{(\omega_T)^2}} \end{array} \] da cui è possibile calcolare la fase \[ \begin{array}{ccl} \angle \underline{H}(\omega) & = & \arctan\left( \frac{\frac{\frac{\omega}{\omega_T}}{1 + \frac{\omega^2}{(\omega_T)^2}}}{\frac{\frac{\omega^2}{(\omega_T)^2}}{1 + \frac{\omega^2}{(\omega_T)^2}}} \right) \\ & = & \arctan\left( \frac{\frac{\omega}{\omega_T}}{\frac{\omega^2}{(\omega_T)^2}} \right) \\ & = & \arctan\left( \frac{1}{\frac{\omega}{\omega_T}} \right) \\ & = & \arctan\left( \frac{\omega_T}{\omega} \right) \\ & \overset{\frac{R}{L} = \omega_T}{=} & \arctan\left( \frac{\frac{R}{L}}{\omega} \right) \\ & = & \arctan\left( \frac{R}{L \cdot \omega} \right) \end{array} \] che graficata è uguale a

Nota bene - Circuito RL come filtro passa-basso
Considerando come uscita la tensione \( \underline{V}_R\), si ha che è possibile utilizzare questo circuito come filtro passa-basso.
Definizione - Filtro passa-banda
Un filtro passa-banda ideale è una rete caratterizzata dalla seguente funzione di trasferimento 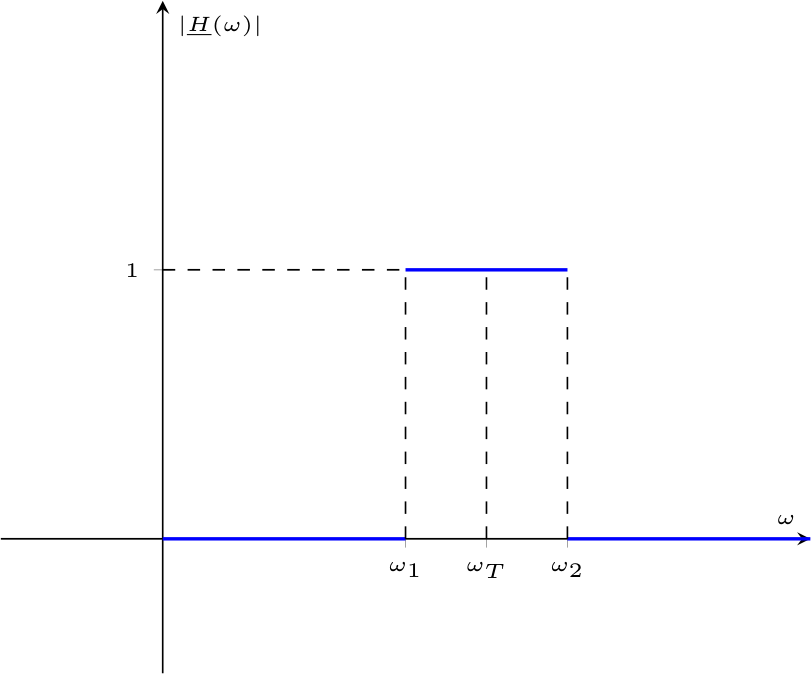 dove \( \omega_T\) è la pulsazione di taglio e la lunghezza dell'intervallo \( [\omega_1, \omega_2]\) è detta ampiezza di banda.
dove \( \omega_T\) è la pulsazione di taglio e la lunghezza dell'intervallo \( [\omega_1, \omega_2]\) è detta ampiezza di banda.
Questo filtro permette il passaggio di segnale ad una frequenza compresa nell'intervallo \( [\omega_1, \omega_2]\) mentre attenua i segnali ad altre frequenze. che, applicando Steinmetz, equivalerebbe al seguente circuito
che, applicando Steinmetz, equivalerebbe al seguente circuito 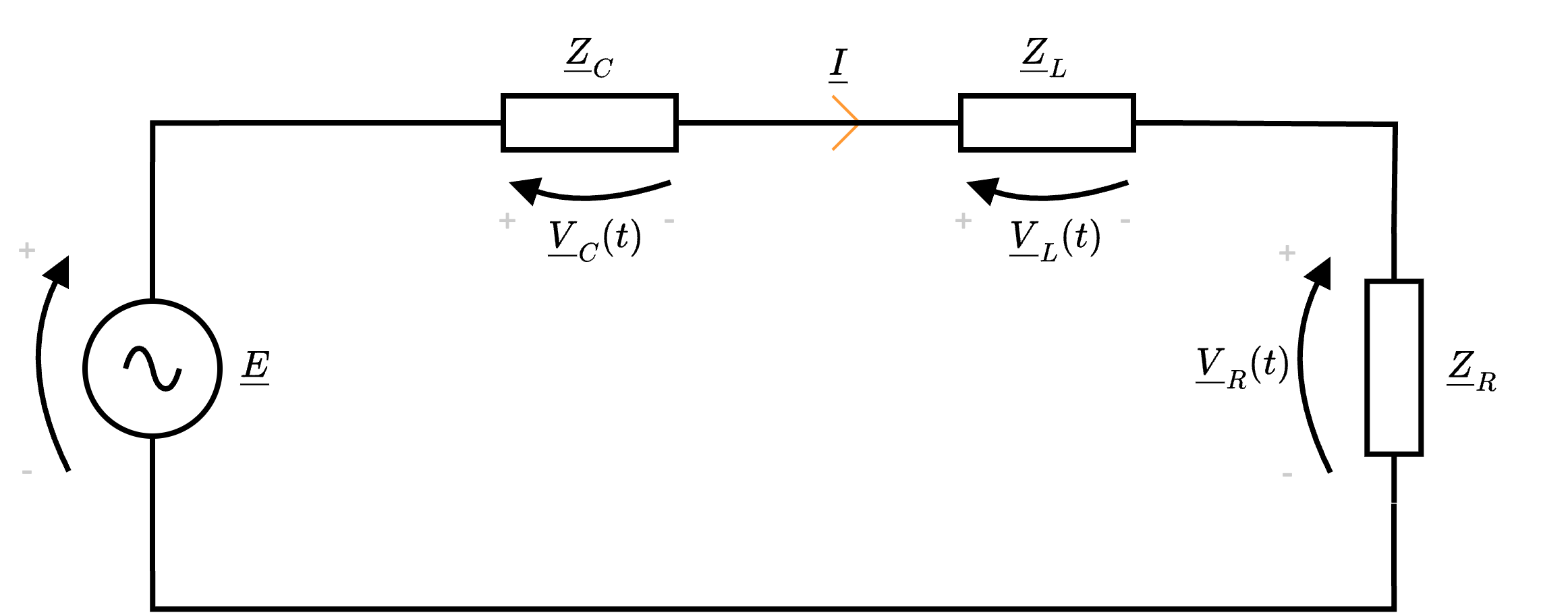 in cui si considera come segnale di ingresso quello del generatore \( \underline{E}\) e come segnale in uscita la tensione ai capi del resistore \( \underline{V}_R\).
in cui si considera come segnale di ingresso quello del generatore \( \underline{E}\) e come segnale in uscita la tensione ai capi del resistore \( \underline{V}_R\).
Calcolando \( \underline{V}_R\), considerando la formula del partitore di tensione, si ha che \[ \begin{array}{ccl} \underline{V}_L & = & \underline{E} \cdot \frac{\underline{Z}_R}{\underline{Z}_R + \underline{Z}_L + \underline{Z}_C} \\ & = & \underline{E} \cdot \frac{R}{R + \jmath \cdot \omega \cdot L - \jmath \cdot \frac{1}{\omega \cdot C}} \\ & = & \underline{E} \cdot \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \end{array} \] è poi possibile calcolare la funzione di trasferimento come \[ \begin{array}{ccl} \underline{H}(\omega) & = & \frac{\underline{V}_R}{\underline{E}} \\ & = & \frac{\underline{E} \cdot \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}}{\underline{E}} \\ & = & \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \\ & \overset{\cdot \frac{R - \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R - \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}}{=} & \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \cdot \frac{R - \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R - \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \\ & = & \frac{R^2 - \jmath \cdot R \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R^2 - \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)^2} \end{array} \] È quindi possibile calcolare il modulo della funzione di trasferimento come \[ \begin{array}{ccl} \left| \underline{H}(\omega) \right| & = & \left| \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \right| \\ & = & \frac{R}{\sqrt{R^2 + \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)^2}} \end{array} \] e considerare la pulsazione di taglio pari a \[ \omega_T = \frac{1}{\sqrt{L \cdot C}} \] Graficando tale relazione, si ottiene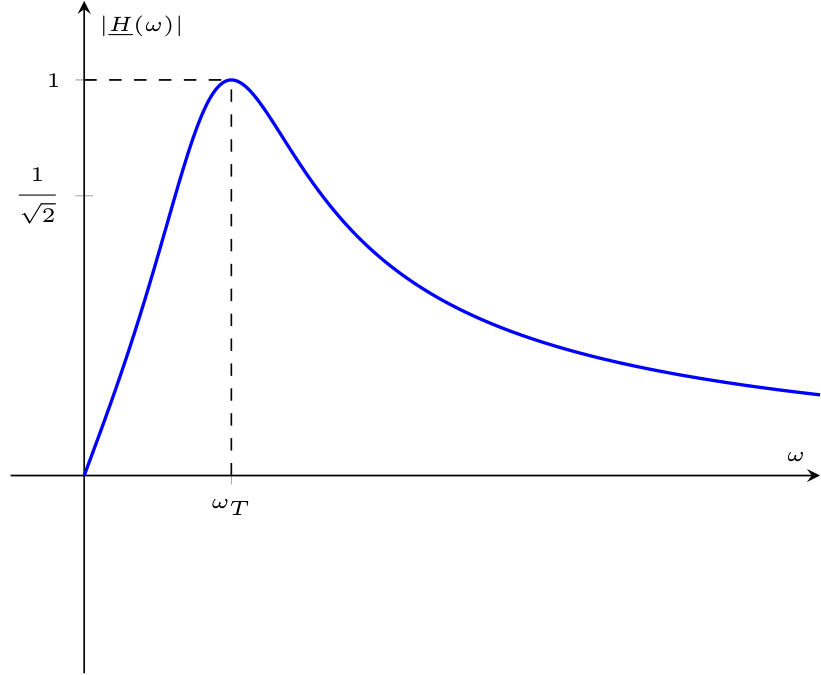 che approssima bene la funzione di trasferimento di un filtro passa-banda ideale.
che approssima bene la funzione di trasferimento di un filtro passa-banda ideale.
Considerando la fase, essa è uguale a \[ \begin{array}{ccl} \angle \underline{H}(\omega) & = & \arctan\left( \frac{\frac{- R \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R^2 - \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)^2}}{\frac{R^2}{R^2 - \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)^2}} \right) \\ & = & \arctan\left( \frac{- R \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R^2} \right) \\ & = & \arctan\left( \frac{\frac{1}{\omega \cdot C} - \omega \cdot L }{R} \right) \\ \end{array} \] che graficata è uguale a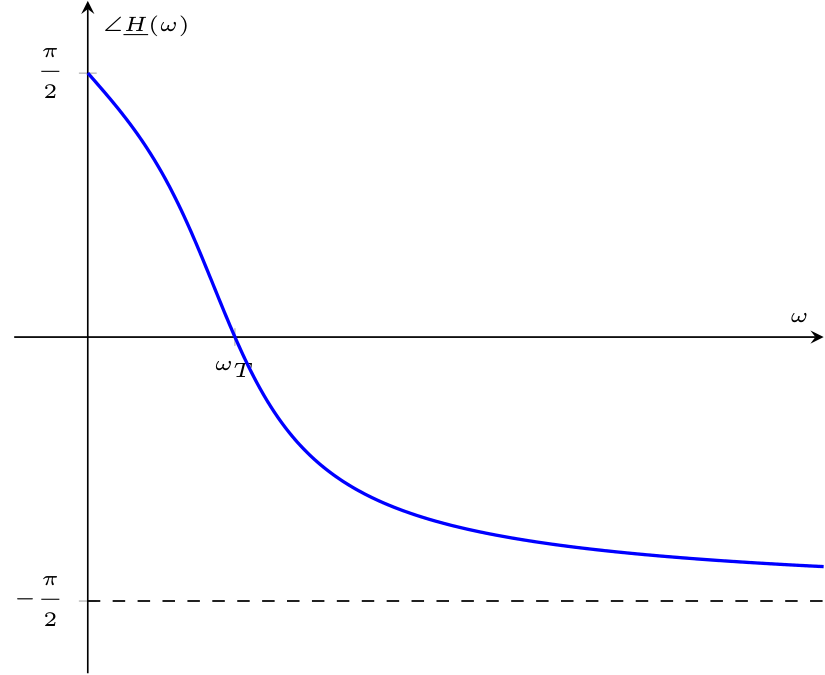

Questo filtro permette il passaggio di segnale ad una frequenza compresa nell'intervallo \( [\omega_1, \omega_2]\) mentre attenua i segnali ad altre frequenze.
Realizzazione di un filtro passa-banda con un circuito RLC
È possibile realizzare un filtro passa-banda per la tensione utilizzando un circuito RLC

Calcolando \( \underline{V}_R\), considerando la formula del partitore di tensione, si ha che \[ \begin{array}{ccl} \underline{V}_L & = & \underline{E} \cdot \frac{\underline{Z}_R}{\underline{Z}_R + \underline{Z}_L + \underline{Z}_C} \\ & = & \underline{E} \cdot \frac{R}{R + \jmath \cdot \omega \cdot L - \jmath \cdot \frac{1}{\omega \cdot C}} \\ & = & \underline{E} \cdot \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \end{array} \] è poi possibile calcolare la funzione di trasferimento come \[ \begin{array}{ccl} \underline{H}(\omega) & = & \frac{\underline{V}_R}{\underline{E}} \\ & = & \frac{\underline{E} \cdot \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}}{\underline{E}} \\ & = & \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \\ & \overset{\cdot \frac{R - \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R - \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}}{=} & \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \cdot \frac{R - \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R - \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \\ & = & \frac{R^2 - \jmath \cdot R \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R^2 - \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)^2} \end{array} \] È quindi possibile calcolare il modulo della funzione di trasferimento come \[ \begin{array}{ccl} \left| \underline{H}(\omega) \right| & = & \left| \frac{R}{R + \jmath \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)} \right| \\ & = & \frac{R}{\sqrt{R^2 + \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)^2}} \end{array} \] e considerare la pulsazione di taglio pari a \[ \omega_T = \frac{1}{\sqrt{L \cdot C}} \] Graficando tale relazione, si ottiene

Considerando la fase, essa è uguale a \[ \begin{array}{ccl} \angle \underline{H}(\omega) & = & \arctan\left( \frac{\frac{- R \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R^2 - \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)^2}}{\frac{R^2}{R^2 - \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)^2}} \right) \\ & = & \arctan\left( \frac{- R \cdot \left( \omega \cdot L - \frac{1}{\omega \cdot C} \right)}{R^2} \right) \\ & = & \arctan\left( \frac{\frac{1}{\omega \cdot C} - \omega \cdot L }{R} \right) \\ \end{array} \] che graficata è uguale a

Nota bene - Circuito RLC come filtro arresta-banda
Considerando come uscita la tensione \( \underline{V}_C + \underline{V}_L\), si ha che è possibile utilizzare questo circuito come filtro arresta-banda.