Definizione - Sistema monofase
Un sistema monofase è un sistema di distribuzione dell'energia elettrica caratterizzato da due conduttori, uno a potenziale nullo (detto neutro) e un conduttore attivo (detto fase).
Definizione - Sistema trifase
Un sistema trifase è un sistema di distribuzione dell'energia elettrica in cui il collegamento è fatto attraverso tre conduttori (dette fasi) 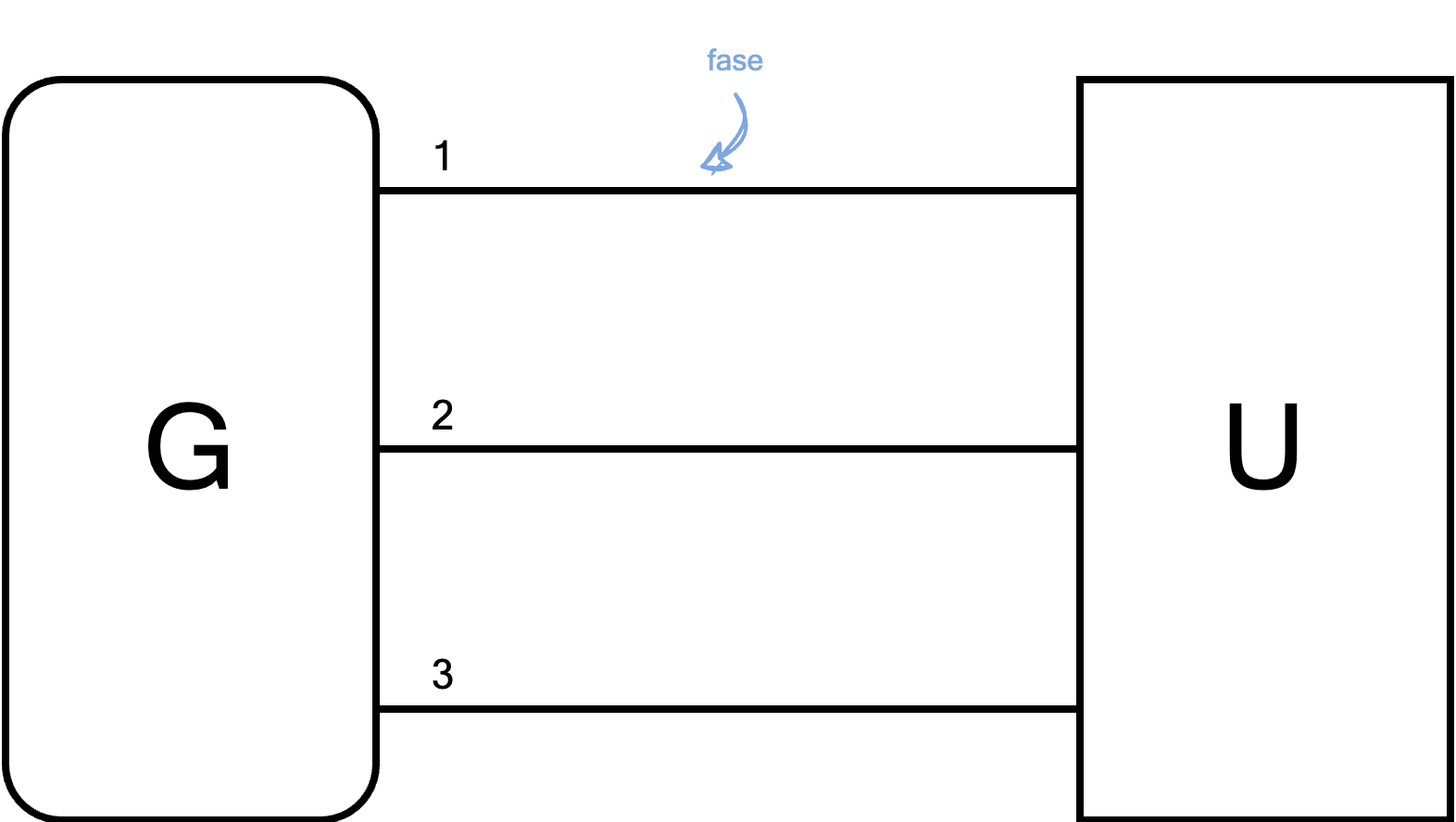

Vantaggi
Tra i motivi di utilizzo di un sistema trifase si ha che:- la quasi totalità di energia elettrica è generata e distribuita da sistemi trifase e, nel settore industriale, buona parte delle macchine elettriche si basano su un campo magnetico rotante, creabile attraverso questo tipo di sistemi;
- la potenza istantanea attiva è costante;
- a parità di potenza trasmessa, è necessario utilizzare meno conduttore rispetto a sistemi monofase.
Definizione - Terna simmetrica
Tre grandezze omogenee si definiscono una terna simmetrica se: 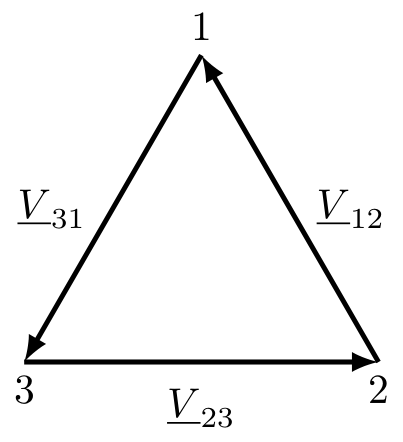 oppure come una terna simmetrica inversa
oppure come una terna simmetrica inversa 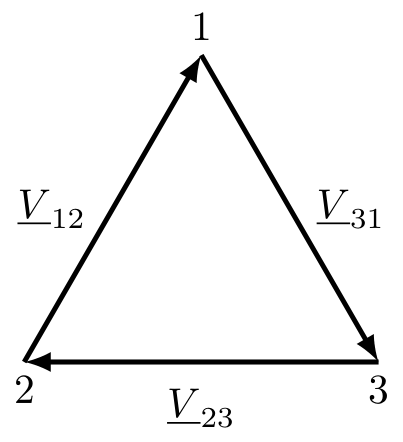
- hanno modulo uguale;
- la loro somma è nulla.
Rappresentazione fasoriale
Considerando una terna simmetrica di fasori \( (\underline{V}_{12}, \underline{V}_{23}, \underline{V}_{31})\), si ha che può essere rappresentata come una terna simmetrica diretta

Definizione - Grandezze in un circuito trifase
Considerando un generico circuito trifase, è possibile individuare diverse grandezze 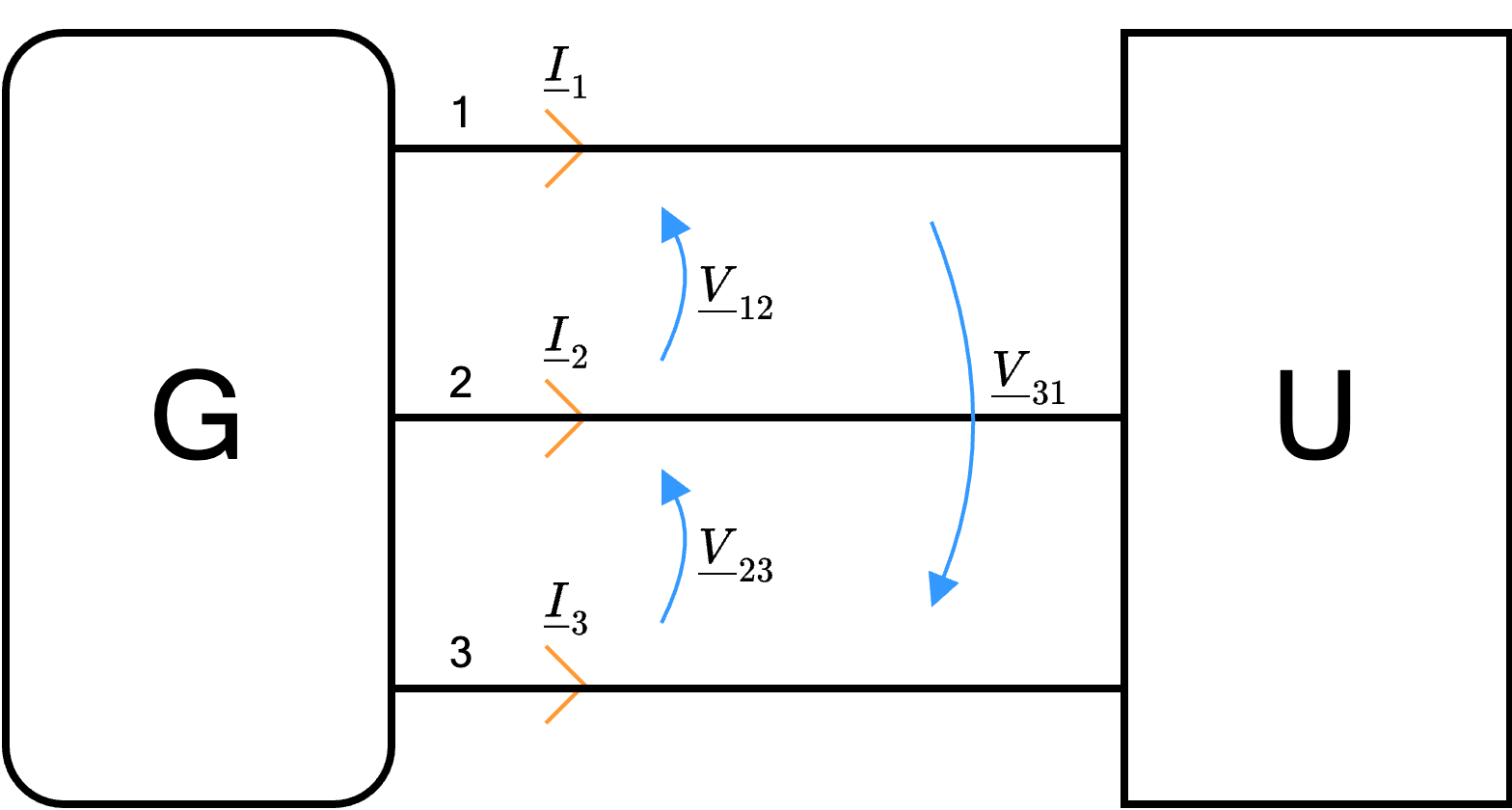 dove le tensioni \( \underline{V}_{12}\), \( \underline{V}_{23}\) e \( \underline{V}_{31}\) sono dette tensioni concatenate e sono caratterizzate da un valore di picco pari a \( \hat{V}\).
dove le tensioni \( \underline{V}_{12}\), \( \underline{V}_{23}\) e \( \underline{V}_{31}\) sono dette tensioni concatenate e sono caratterizzate da un valore di picco pari a \( \hat{V}\).
Applicando LKT è possibile ottenere che \[ LKT: \quad \underline{V}_{12} + \underline{V}_{23} + \underline{V}_{31} = 0 \] ovvero è possibile considerare che le tensioni sono una terna simmetrica.
È quindi possibile ridisegnare i fasori nel piano complesso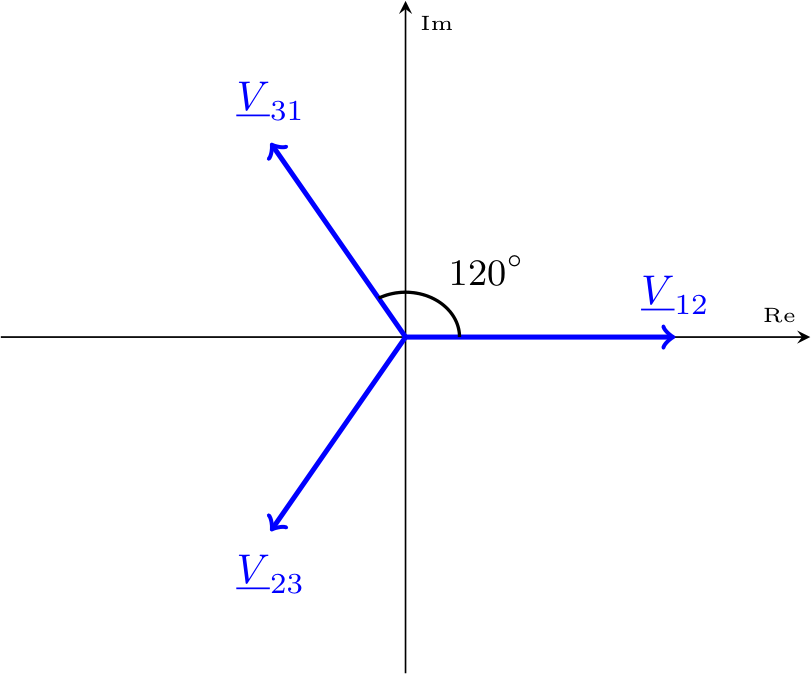 ottenendo tre fasori sfasati di \( 120^\circ\) (in radianti \( \; {}^{2} /_{3\;}\pi\)) uguali a \[ \left\{ \begin{array}{ccl} \underline{V}_{12} & = & \hat{V} \cdot \mathrm{e}^{\jmath \cdot 0} \\ \underline{V}_{31} & = & \hat{V} \cdot \mathrm{e}^{\jmath \cdot \; {}^{2} /_{3\;}\pi} \\ \underline{V}_{23} & = & \hat{V} \cdot \mathrm{e}^{\jmath \cdot \left( -\; {}^{2} /_{3\;}\pi \right)} \end{array} \right. \] Considerando come riferimento il fasore \( \underline{V}_{12}\), si ha che è possibile scrivere gli altri fasori della terna in sua funzione, ottenendo \[ \left\{ \begin{array}{ccl} \underline{V}_{31} & = & \underline{V}_{12} \cdot \mathrm{e}^{\jmath \cdot \; {}^{2} /_{3\;}\pi} \\ \underline{V}_{23} & = & \underline{V}_{12} \cdot \mathrm{e}^{\jmath \cdot \left( -\; {}^{2} /_{3\;}\pi \right)} \end{array} \right. \]
ottenendo tre fasori sfasati di \( 120^\circ\) (in radianti \( \; {}^{2} /_{3\;}\pi\)) uguali a \[ \left\{ \begin{array}{ccl} \underline{V}_{12} & = & \hat{V} \cdot \mathrm{e}^{\jmath \cdot 0} \\ \underline{V}_{31} & = & \hat{V} \cdot \mathrm{e}^{\jmath \cdot \; {}^{2} /_{3\;}\pi} \\ \underline{V}_{23} & = & \hat{V} \cdot \mathrm{e}^{\jmath \cdot \left( -\; {}^{2} /_{3\;}\pi \right)} \end{array} \right. \] Considerando come riferimento il fasore \( \underline{V}_{12}\), si ha che è possibile scrivere gli altri fasori della terna in sua funzione, ottenendo \[ \left\{ \begin{array}{ccl} \underline{V}_{31} & = & \underline{V}_{12} \cdot \mathrm{e}^{\jmath \cdot \; {}^{2} /_{3\;}\pi} \\ \underline{V}_{23} & = & \underline{V}_{12} \cdot \mathrm{e}^{\jmath \cdot \left( -\; {}^{2} /_{3\;}\pi \right)} \end{array} \right. \]

Applicando LKT è possibile ottenere che \[ LKT: \quad \underline{V}_{12} + \underline{V}_{23} + \underline{V}_{31} = 0 \] ovvero è possibile considerare che le tensioni sono una terna simmetrica.
È quindi possibile ridisegnare i fasori nel piano complesso

Definizione - Modello di un generatore in un sistema trifase
Considerando un generatore G in un sistema trifase è possibile rappresentarlo nel seguente modo 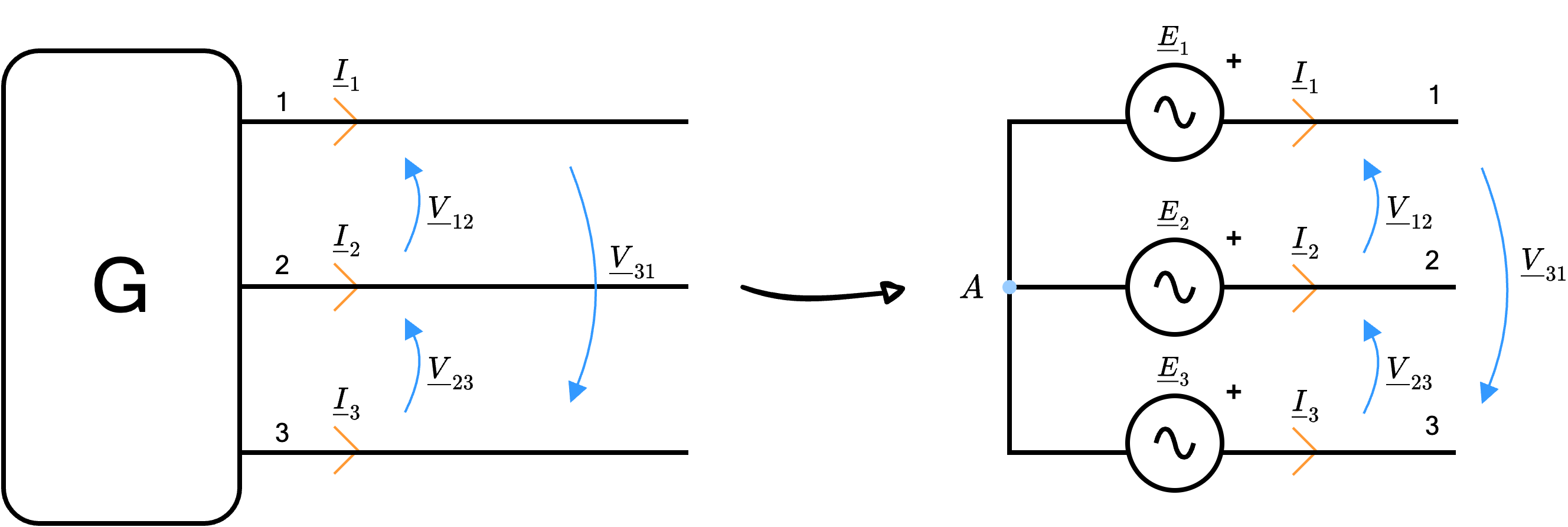 dove i fasori \( \underline{E}_1\), \( \underline{E}_2\) ed \( \underline{E}_3\) sono dette tensioni di fase.
dove i fasori \( \underline{E}_1\), \( \underline{E}_2\) ed \( \underline{E}_3\) sono dette tensioni di fase.
Applicando LKT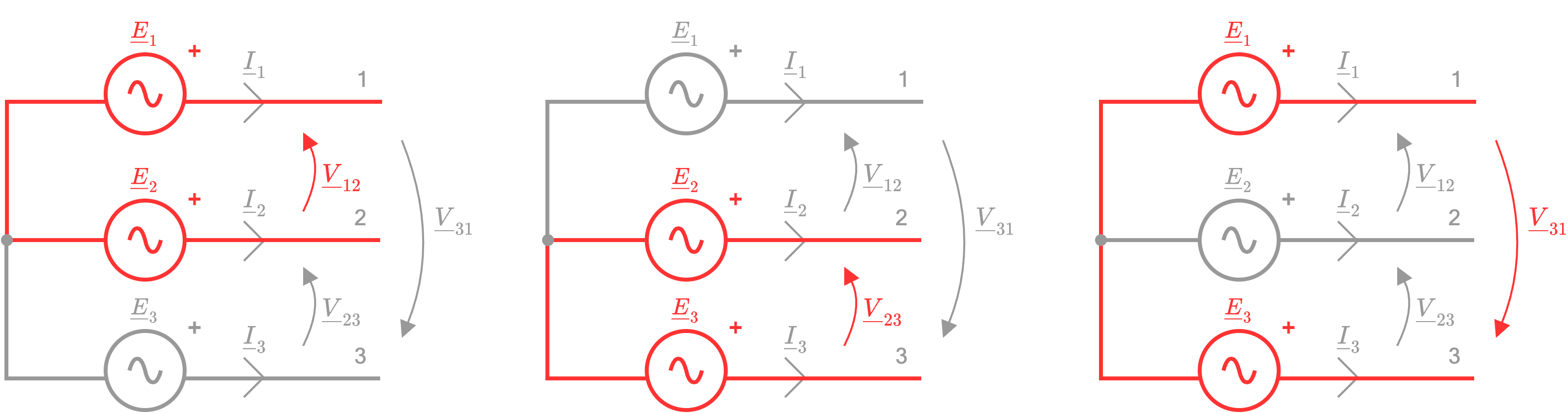 è possibile ottenere le seguenti equazioni \[ \left\{ \begin{array}{ccl} \underline{V}_{12} & = & \underline{E}_1 - \underline{E}_2 \\ \underline{V}_{23} & = & \underline{E}_2 - \underline{E}_3 \\ \underline{V}_{31} & = & \underline{E}_3 - \underline{E}_1 \end{array} \right. \] che nella rappresentazione della terna simmetrica diretta sarebbero uguali a
è possibile ottenere le seguenti equazioni \[ \left\{ \begin{array}{ccl} \underline{V}_{12} & = & \underline{E}_1 - \underline{E}_2 \\ \underline{V}_{23} & = & \underline{E}_2 - \underline{E}_3 \\ \underline{V}_{31} & = & \underline{E}_3 - \underline{E}_1 \end{array} \right. \] che nella rappresentazione della terna simmetrica diretta sarebbero uguali a 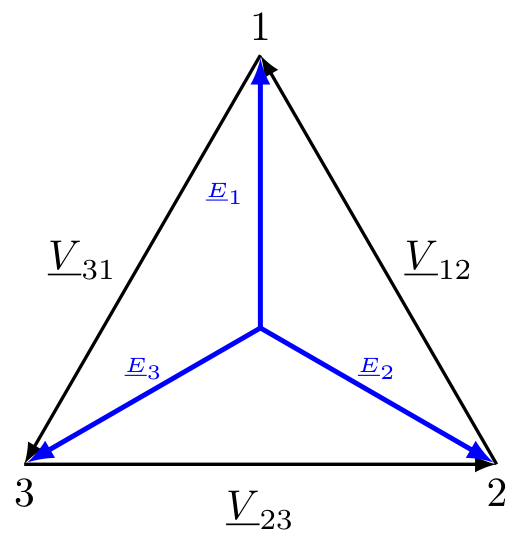 Dato che i fasori delle tensioni concatenate formano un triangolo equilatero (ndr, hanno stesso modulo dato che sono una terna simmetrica) è possibile dimostrare che anche le tensioni concatenate formano una terna simmetrica e che vale \[ V = \sqrt{3} \cdot E \] ovvero che vi è una relazione tra il modulo \( V\) delle tensioni concatenate ed il modulo \( E\) delle tensioni di fase.
Dato che i fasori delle tensioni concatenate formano un triangolo equilatero (ndr, hanno stesso modulo dato che sono una terna simmetrica) è possibile dimostrare che anche le tensioni concatenate formano una terna simmetrica e che vale \[ V = \sqrt{3} \cdot E \] ovvero che vi è una relazione tra il modulo \( V\) delle tensioni concatenate ed il modulo \( E\) delle tensioni di fase.

Applicando LKT


Definizione - Modello di un carico in un sistema trifase
Considerando un carico U in un sistema trifase è possibile modellarlo come un insieme di impedenze.
In base alle connessioni tra le impedenze, è possibile considerare la connessione a stella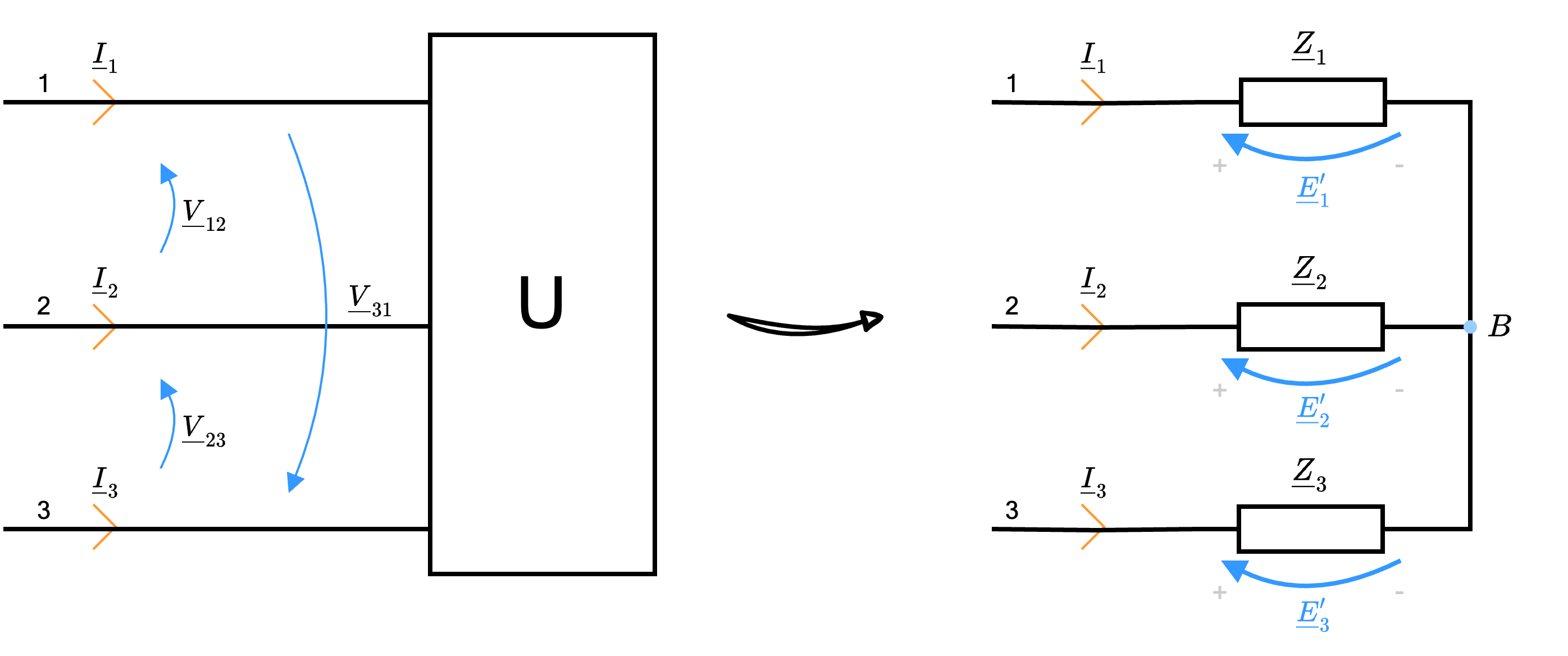 e la connessione a triangolo
e la connessione a triangolo  Al fine di calcolare le tensioni \( \underline{E}_1'\), \( \underline{E}_2'\) e \( \underline{E}_3'\) nel caso del collegamento a stella, consideriamo la tensione \( \underline{V}_{AB}\)
Al fine di calcolare le tensioni \( \underline{E}_1'\), \( \underline{E}_2'\) e \( \underline{E}_3'\) nel caso del collegamento a stella, consideriamo la tensione \( \underline{V}_{AB}\) 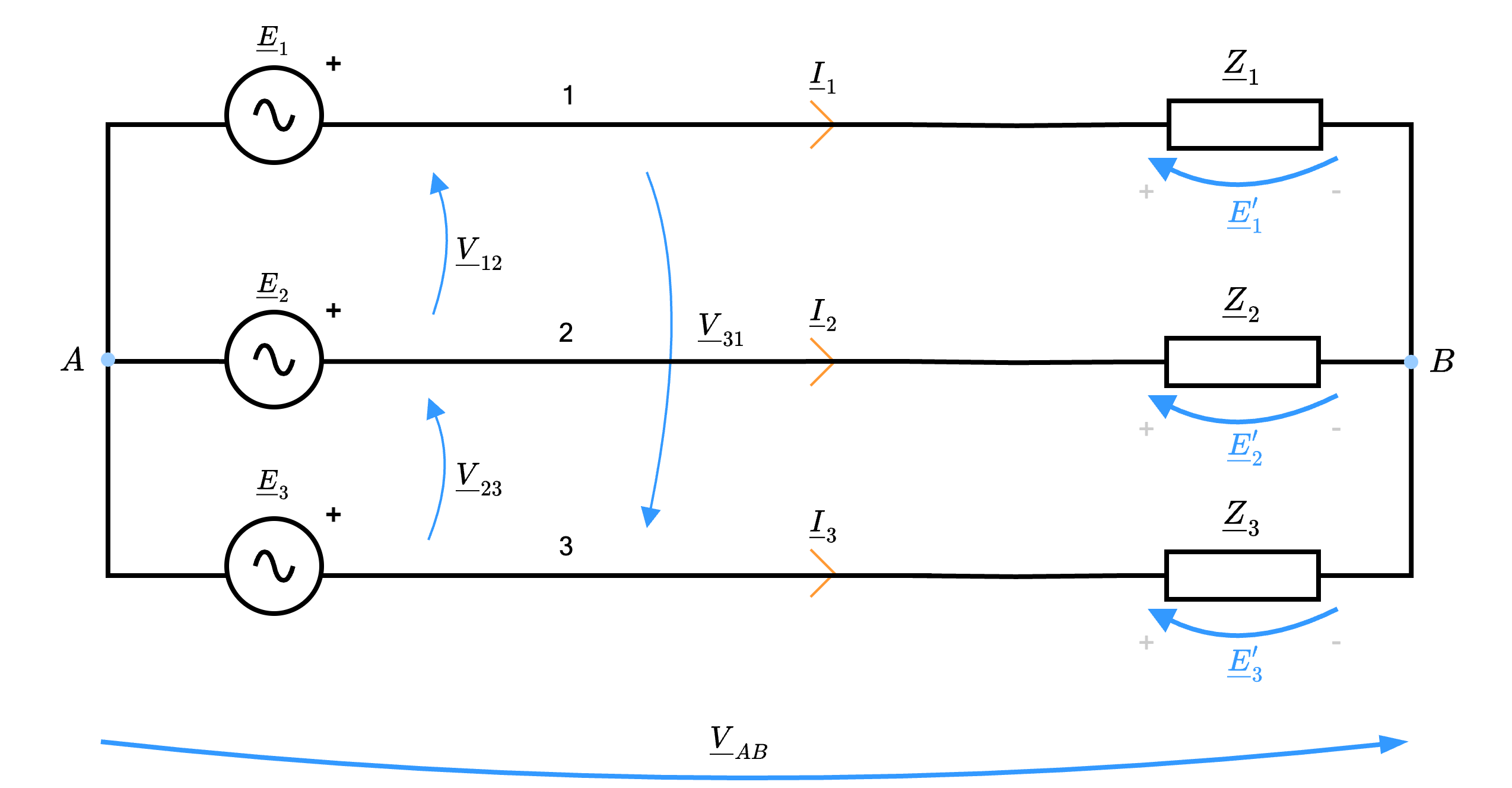 e applichiamo LKT per ottenere \[ \left\{ \begin{array}{lcl} \underline{E}_1 - \underline{E}_1' - \underline{V}_{AB} & = & 0 \\ \underline{E}_2 - \underline{E}_2' - \underline{V}_{AB} & = & 0 \\ \underline{E}_3 - \underline{E}_3' - \underline{V}_{AB} & = & 0 \end{array} \right. \quad \implies \quad \left\{ \begin{array}{ccl} \underline{E}_1' & = & \underline{E}_1 - \underline{V}_{AB} \\ \underline{E}_2' & = & \underline{E}_2 - \underline{V}_{AB} \\ \underline{E}_3' & = & \underline{E}_3 - \underline{V}_{AB} \\ \end{array} \right. \] Considerando la terna diretta, è possibile ipotizzare che \( \underline{V}_{AB}\) non sia nulla, ottenendo
e applichiamo LKT per ottenere \[ \left\{ \begin{array}{lcl} \underline{E}_1 - \underline{E}_1' - \underline{V}_{AB} & = & 0 \\ \underline{E}_2 - \underline{E}_2' - \underline{V}_{AB} & = & 0 \\ \underline{E}_3 - \underline{E}_3' - \underline{V}_{AB} & = & 0 \end{array} \right. \quad \implies \quad \left\{ \begin{array}{ccl} \underline{E}_1' & = & \underline{E}_1 - \underline{V}_{AB} \\ \underline{E}_2' & = & \underline{E}_2 - \underline{V}_{AB} \\ \underline{E}_3' & = & \underline{E}_3 - \underline{V}_{AB} \\ \end{array} \right. \] Considerando la terna diretta, è possibile ipotizzare che \( \underline{V}_{AB}\) non sia nulla, ottenendo 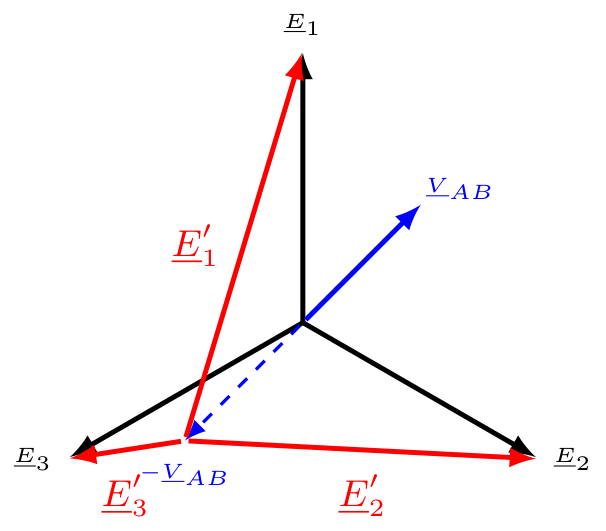 È evidente che, affinché \( \left( \underline{E}_1', \underline{E}_2', \underline{E}_3' \right)\) sia una terna simmetrica, occorre che la tensione \( \underline{V}_{AB}\) sia nulla.
È evidente che, affinché \( \left( \underline{E}_1', \underline{E}_2', \underline{E}_3' \right)\) sia una terna simmetrica, occorre che la tensione \( \underline{V}_{AB}\) sia nulla.
Algebricamente si ha infatti che, considerando di applicare LKC, si ottiene \[ \begin{array}{lc} \underline{I}_1 + \underline{I}_2 + \underline{I}_3 = 0 & \iff \\ \frac{\underline{E}_1 - \underline{V}_{AB}}{\underline{Z}_1} + \frac{\underline{E}_2 - \underline{V}_{AB}}{\underline{Z}_2} + \frac{\underline{E}_3 - \underline{V}_{AB}}{\underline{Z}_3} = 0 & \end{array} \] e, risolvendo l'equazione per \( \underline{V}_{AB}\) \begin{aligned} & \frac{\underline{E}_1 - \underline{V}_{AB}}{\underline{Z}_1} + \frac{\underline{E}_2 - \underline{V}_{AB}}{\underline{Z}_2} + \frac{\underline{E}_3 - \underline{V}_{AB}}{\underline{Z}_3} = 0 & \iff \\ & \frac{\underline{E}_1}{\underline{Z}_1} - \frac{\underline{V}_{AB}}{\underline{Z}_1} + \frac{\underline{E}_2}{\underline{Z}_2} - \frac{\underline{V}_{AB}}{\underline{Z}_2} + \frac{\underline{E}_3}{\underline{Z}_3} - \frac{\underline{V}_{AB}}{\underline{Z}_3} = 0 & \iff \\ & \frac{\underline{V}_{AB}}{\underline{Z}_1} + \frac{\underline{V}_{AB}}{\underline{Z}_2} + \frac{\underline{V}_{AB}}{\underline{Z}_3} = \frac{\underline{E}_1}{\underline{Z}_1} + \frac{\underline{E}_2}{\underline{Z}_2} + \frac{\underline{E}_3}{\underline{Z}_3} & \iff \\ & \underline{V}_{AB} \cdot \left( \frac{1}{\underline{Z}_1} + \frac{1}{\underline{Z}_2} + \frac{1}{\underline{Z}_3} \right) = \frac{\underline{E}_1}{\underline{Z}_1} + \frac{\underline{E}_2}{\underline{Z}_2} + \frac{\underline{E}_3}{\underline{Z}_3} & \iff \\ & \underline{V}_{AB} = \frac{\; {}^{\underline{E}_1} /_{\underline{Z}_1\;} + \; {}^{\underline{E}_2} /_{\underline{Z}_2\;} + \; {}^{\underline{E}_3} /_{\underline{Z}_3\;}}{\; {}^{1} /_{\underline{Z}\;_1} + \; {}^{1} /_{\underline{Z}\;_2} + \; {}^{1} /_{\underline{Z}\;_3}} & \end{aligned} Ciò evidenzia il fatto che solo nel caso di un carico equilibrato (le cui impedenze hanno modulo uguale) si avrebbe una tensione \( \underline{V}_{AB}\) nulla, infatti \[ \begin{array}{ccl} \underline{V}_{AB} & = & \frac{\; {}^{\underline{E}_1} /_{\underline{Z}_1\;} + \; {}^{\underline{E}_2} /_{\underline{Z}_2\;} + \; {}^{\underline{E}_3} /_{\underline{Z}_3\;}}{\; {}^{1} /_{\underline{Z}\;_1} + \; {}^{1} /_{\underline{Z}\;_2} + \; {}^{1} /_{\underline{Z}\;_3}} \\ & \overset{\underline{Z} = \underline{Z}_1 = \underline{Z}_2 = \underline{Z}_3}{=} & \frac{\; {}^{\underline{E}_1} /_{\underline{Z}\;} + \; {}^{\underline{E}_2} /_{\underline{Z}\;} + \; {}^{\underline{E}_3} /_{\underline{Z}\;}}{\; {}^{1} /_{\underline{Z}\;} + \; {}^{1} /_{\underline{Z}\;} + \; {}^{1} /_{\underline{Z}\;}} \\ & = & \frac{\; {}^{1} /_{\underline{Z}\;} \cdot \overbrace{\left( \underline{E}_1 + \underline{E}_2 + \underline{E}_3 \right)}^0}{\; {}^{1} /_{\underline{Z}\;} + \; {}^{1} /_{\underline{Z}\;} + \; {}^{1} /_{\underline{Z}\;}} \\ & = & 0 \end{array} \] Inoltre, con un carico equilibrato, si ha che anche la terna delle correnti è una terna simmetrica. si avrebbe:
si avrebbe:
In base alle connessioni tra le impedenze, è possibile considerare la connessione a stella




Algebricamente si ha infatti che, considerando di applicare LKC, si ottiene \[ \begin{array}{lc} \underline{I}_1 + \underline{I}_2 + \underline{I}_3 = 0 & \iff \\ \frac{\underline{E}_1 - \underline{V}_{AB}}{\underline{Z}_1} + \frac{\underline{E}_2 - \underline{V}_{AB}}{\underline{Z}_2} + \frac{\underline{E}_3 - \underline{V}_{AB}}{\underline{Z}_3} = 0 & \end{array} \] e, risolvendo l'equazione per \( \underline{V}_{AB}\) \begin{aligned} & \frac{\underline{E}_1 - \underline{V}_{AB}}{\underline{Z}_1} + \frac{\underline{E}_2 - \underline{V}_{AB}}{\underline{Z}_2} + \frac{\underline{E}_3 - \underline{V}_{AB}}{\underline{Z}_3} = 0 & \iff \\ & \frac{\underline{E}_1}{\underline{Z}_1} - \frac{\underline{V}_{AB}}{\underline{Z}_1} + \frac{\underline{E}_2}{\underline{Z}_2} - \frac{\underline{V}_{AB}}{\underline{Z}_2} + \frac{\underline{E}_3}{\underline{Z}_3} - \frac{\underline{V}_{AB}}{\underline{Z}_3} = 0 & \iff \\ & \frac{\underline{V}_{AB}}{\underline{Z}_1} + \frac{\underline{V}_{AB}}{\underline{Z}_2} + \frac{\underline{V}_{AB}}{\underline{Z}_3} = \frac{\underline{E}_1}{\underline{Z}_1} + \frac{\underline{E}_2}{\underline{Z}_2} + \frac{\underline{E}_3}{\underline{Z}_3} & \iff \\ & \underline{V}_{AB} \cdot \left( \frac{1}{\underline{Z}_1} + \frac{1}{\underline{Z}_2} + \frac{1}{\underline{Z}_3} \right) = \frac{\underline{E}_1}{\underline{Z}_1} + \frac{\underline{E}_2}{\underline{Z}_2} + \frac{\underline{E}_3}{\underline{Z}_3} & \iff \\ & \underline{V}_{AB} = \frac{\; {}^{\underline{E}_1} /_{\underline{Z}_1\;} + \; {}^{\underline{E}_2} /_{\underline{Z}_2\;} + \; {}^{\underline{E}_3} /_{\underline{Z}_3\;}}{\; {}^{1} /_{\underline{Z}\;_1} + \; {}^{1} /_{\underline{Z}\;_2} + \; {}^{1} /_{\underline{Z}\;_3}} & \end{aligned} Ciò evidenzia il fatto che solo nel caso di un carico equilibrato (le cui impedenze hanno modulo uguale) si avrebbe una tensione \( \underline{V}_{AB}\) nulla, infatti \[ \begin{array}{ccl} \underline{V}_{AB} & = & \frac{\; {}^{\underline{E}_1} /_{\underline{Z}_1\;} + \; {}^{\underline{E}_2} /_{\underline{Z}_2\;} + \; {}^{\underline{E}_3} /_{\underline{Z}_3\;}}{\; {}^{1} /_{\underline{Z}\;_1} + \; {}^{1} /_{\underline{Z}\;_2} + \; {}^{1} /_{\underline{Z}\;_3}} \\ & \overset{\underline{Z} = \underline{Z}_1 = \underline{Z}_2 = \underline{Z}_3}{=} & \frac{\; {}^{\underline{E}_1} /_{\underline{Z}\;} + \; {}^{\underline{E}_2} /_{\underline{Z}\;} + \; {}^{\underline{E}_3} /_{\underline{Z}\;}}{\; {}^{1} /_{\underline{Z}\;} + \; {}^{1} /_{\underline{Z}\;} + \; {}^{1} /_{\underline{Z}\;}} \\ & = & \frac{\; {}^{1} /_{\underline{Z}\;} \cdot \overbrace{\left( \underline{E}_1 + \underline{E}_2 + \underline{E}_3 \right)}^0}{\; {}^{1} /_{\underline{Z}\;} + \; {}^{1} /_{\underline{Z}\;} + \; {}^{1} /_{\underline{Z}\;}} \\ & = & 0 \end{array} \] Inoltre, con un carico equilibrato, si ha che anche la terna delle correnti è una terna simmetrica.
Conseguenze di \( \underline{V}_{AB} \neq 0\)
Nel caso \( \underline{V}_{AB}\) non sia nullo
- della sovratensione, dato che \( \left| \underline{E}_1' \right| \gt \left| \underline{E}_1 \right|\) e che \( \left| \underline{E}_2' \right| \gt \left| \underline{E}_2 \right|\);
- un malfunzionamento, dato che \( \left| \underline{E}_2' \right| \lt \left| \underline{E}_2 \right|\).
Definizione - Sistema trifase a 4 conduttori
Dato che nella realtà non è possibile garantire un carico equilibrato, è possibile considerare di inserire un neutro (un cortocircuito) tra i due nodi, in modo da garantire una differenza di potenziale nulla 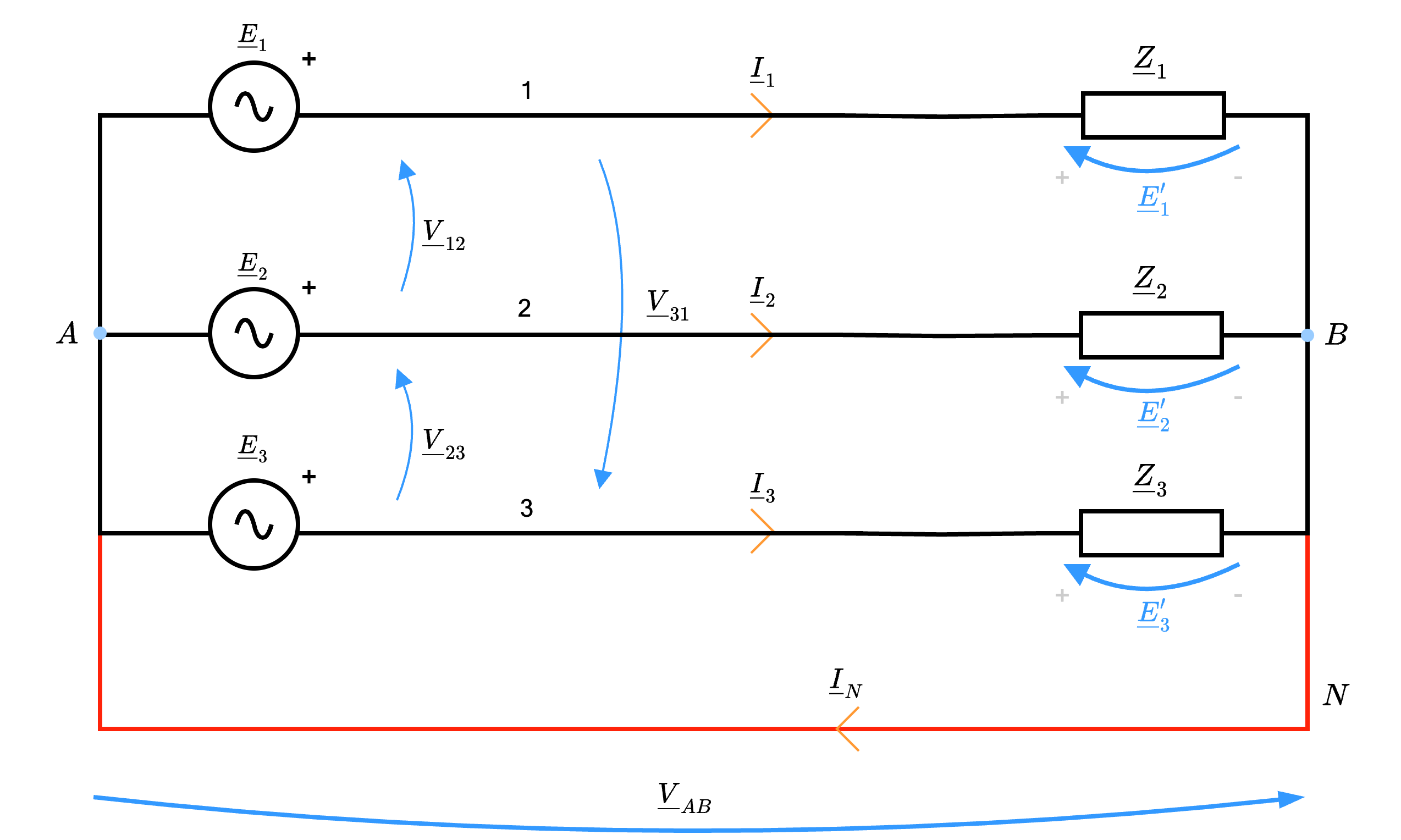 in modo da garantire che le tensioni \( \underline{E}_1'\), \( \underline{E}_2'\) ed \( \underline{E}_3'\) siano una terna simmetrica.
in modo da garantire che le tensioni \( \underline{E}_1'\), \( \underline{E}_2'\) ed \( \underline{E}_3'\) siano una terna simmetrica.
È da notare tuttavia che la presenza del neutro N comporta la presenza di un'ulteriore corrente. Infatti, applicando LKC, si ottiene \[ \begin{array}{ccl} \underline{I}_N & = & \underline{I}_1 + \underline{I}_2 + \underline{I}_3 \\ & = & \frac{\underline{E}_1}{\underline{Z}_1} + \frac{\underline{E}_2}{\underline{Z}_2} + \frac{\underline{E}_3}{\underline{Z}_3} \end{array} \] Da ciò è possibile dedurre che più il carico è squilibrato, maggiore sarà la corrente \( \underline{I}_N\) comportando maggiori perdite dovute a effetto Joule.

È da notare tuttavia che la presenza del neutro N comporta la presenza di un'ulteriore corrente. Infatti, applicando LKC, si ottiene \[ \begin{array}{ccl} \underline{I}_N & = & \underline{I}_1 + \underline{I}_2 + \underline{I}_3 \\ & = & \frac{\underline{E}_1}{\underline{Z}_1} + \frac{\underline{E}_2}{\underline{Z}_2} + \frac{\underline{E}_3}{\underline{Z}_3} \end{array} \] Da ciò è possibile dedurre che più il carico è squilibrato, maggiore sarà la corrente \( \underline{I}_N\) comportando maggiori perdite dovute a effetto Joule.
Definizione - Potenza in sistemi trifase
Considerando un sistema trifase con carico equilibrato  è possibile calcolare la potenza assorbita dal carico U come \[ \begin{array}{ccl} \underline{N} & = & \underline{V} \cdot \underline{I}^* \\ & = & \left( \underline{E}_1 + \underline{E}_2 + \underline{E}_3 \right) \cdot \left( \underline{I}_1^* + \underline{I}_2^* + \underline{I}_3^* \right) \\ & = & \underline{E}_1 \cdot \underline{I}_1^* + \underline{E}_2 \cdot \underline{I}_2^* + \underline{E}_3 \cdot \underline{I}_3^* \\ & \overset{\underline{E} = \underline{E}_1 = \underline{E}_2 = \underline{E}_3}{=} & \underline{E} \cdot \underline{I}_1^* + \underline{E} \cdot \underline{I}_2^* + \underline{E} \cdot \underline{I}_3^* \\ & \overset{\underline{I} = \underline{I}_1 = \underline{I}_2 = \underline{I}_3}{=} & \underline{E} \cdot \underline{I}^* + \underline{E} \cdot \underline{I}^* + \underline{E} \cdot \underline{I}^* \\ & = & 3 \cdot \underline{E} \cdot \underline{I}^* \\ & = & 3 \cdot \left( E \cdot \mathrm{e}^{\jmath \cdot \alpha_V} \right) \cdot \left( I \cdot \mathrm{e}^{-\jmath \cdot \alpha_I} \right) \\ & = & 3 \cdot E \cdot I \cdot \mathrm{e}^{\jmath \cdot \varphi} \\ & = & \overbrace{\sqrt{3} \cdot E}^V \cdot \sqrt{3} \cdot I \cdot \left[ \cos(\varphi) + \jmath \cdot \sin(\varphi) \right] \\ & = & \underbrace{\sqrt{3} \cdot V \cdot I \cdot \cos(\varphi)}_N + \jmath \cdot \underbrace{\sqrt{3} \cdot V \cdot I \cdot \sin(\varphi)}_Q \end{array} \] da cui è possibile dedurre i valori di potenza attiva \( N\) e di potenza reattiva \( Q\) \[ \left\{ \begin{array}{ccl} N & = & \sqrt{3} \cdot V \cdot I \cdot \cos(\varphi) \\ Q & = & \sqrt{3} \cdot V \cdot I \cdot \sin(\varphi) \end{array} \right. \]
è possibile calcolare la potenza assorbita dal carico U come \[ \begin{array}{ccl} \underline{N} & = & \underline{V} \cdot \underline{I}^* \\ & = & \left( \underline{E}_1 + \underline{E}_2 + \underline{E}_3 \right) \cdot \left( \underline{I}_1^* + \underline{I}_2^* + \underline{I}_3^* \right) \\ & = & \underline{E}_1 \cdot \underline{I}_1^* + \underline{E}_2 \cdot \underline{I}_2^* + \underline{E}_3 \cdot \underline{I}_3^* \\ & \overset{\underline{E} = \underline{E}_1 = \underline{E}_2 = \underline{E}_3}{=} & \underline{E} \cdot \underline{I}_1^* + \underline{E} \cdot \underline{I}_2^* + \underline{E} \cdot \underline{I}_3^* \\ & \overset{\underline{I} = \underline{I}_1 = \underline{I}_2 = \underline{I}_3}{=} & \underline{E} \cdot \underline{I}^* + \underline{E} \cdot \underline{I}^* + \underline{E} \cdot \underline{I}^* \\ & = & 3 \cdot \underline{E} \cdot \underline{I}^* \\ & = & 3 \cdot \left( E \cdot \mathrm{e}^{\jmath \cdot \alpha_V} \right) \cdot \left( I \cdot \mathrm{e}^{-\jmath \cdot \alpha_I} \right) \\ & = & 3 \cdot E \cdot I \cdot \mathrm{e}^{\jmath \cdot \varphi} \\ & = & \overbrace{\sqrt{3} \cdot E}^V \cdot \sqrt{3} \cdot I \cdot \left[ \cos(\varphi) + \jmath \cdot \sin(\varphi) \right] \\ & = & \underbrace{\sqrt{3} \cdot V \cdot I \cdot \cos(\varphi)}_N + \jmath \cdot \underbrace{\sqrt{3} \cdot V \cdot I \cdot \sin(\varphi)}_Q \end{array} \] da cui è possibile dedurre i valori di potenza attiva \( N\) e di potenza reattiva \( Q\) \[ \left\{ \begin{array}{ccl} N & = & \sqrt{3} \cdot V \cdot I \cdot \cos(\varphi) \\ Q & = & \sqrt{3} \cdot V \cdot I \cdot \sin(\varphi) \end{array} \right. \]
