Definizione - Metodo di risoluzione simbolico
Considerando una rete in regime sinusoidale, si ha che il metodo di risoluzione simbolico consiste nell'applicare la trasformata di Steinmetz alle equazioni differenziali al fine di ottenere equazioni algebriche più semplici da risolvere.
Definizione - Legge di Kirchhoff per le tensioni in forma simbolica (LKT)
Considerando una maglia in una rete a regime sinusoidale, la sommatoria dei fasori delle tensioni di tutti i componenti è nulla, ovvero \[ \sum_{i = 1}^{\# \ \text{componenti}} \underline{V}_i(t) = 0 \qquad \forall t \]
Definizione - Legge di Kirchhoff per le correnti in forma simbolica (LKC)
Considerando una superficie chiusa (ad esempio i nodi) in una rete a regime sinusoidale, la sommatoria dei fasori delle correnti entranti è uguale alla sommatoria dei fasori delle correnti uscenti, ovvero \[ \sum_{j = 1}^{\# \ \text{entranti}} \underline{I}_j(t) = \sum_{k = 1}^{\# \ \text{uscenti}} \underline{I}_k(t) \qquad \forall t \] o, in maniera equivalente \[ \sum_{j = 1}^{\# \ \text{correnti}} \pm \underline{I}_j(t) = 0 \qquad \forall t \]
Definizione - Generatore ideale di tensione sinusoidale
Il generatore ideale di tensione sinusoidale, il cui simbolo è il seguente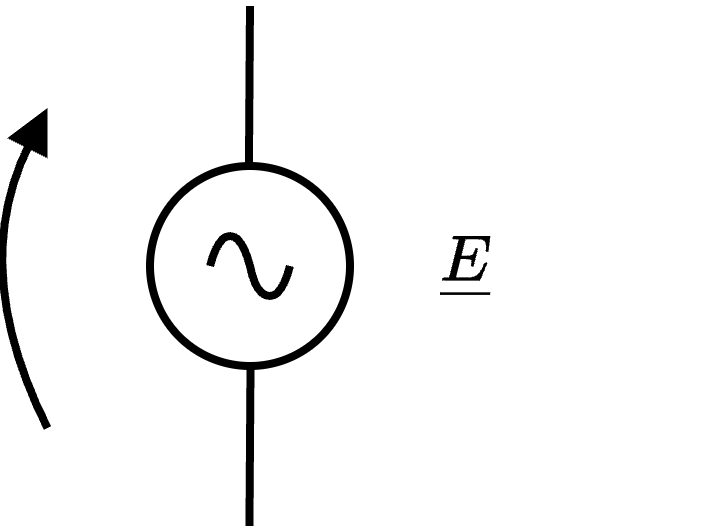 
è un bipolo che permette di "imporre" una tensione pari a \[ v(t) = \sqrt{2} \cdot E \cdot \cos(\omega \cdot t + \alpha) \] e, applicando la trasformata di Steinmetz si ottiene il seguente fasore associato \[ \begin{array}{ccl} S[v(t)] & = & \sqrt{2} \cdot E \cdot \cos(\omega \cdot t + \alpha) \\ & = & \underline{E} \end{array} \]
Definizione - Generatore ideale di corrente sinusoidale
Il generatore ideale di corrente sinusoidale è un bipolo che permette di "imporre" una corrente pari a \[ i(t) = \sqrt{2} \cdot I \cdot \cos(\omega \cdot t + \alpha) \] e, applicando la trasformata di Steinmetz si ottiene il seguente fasore associato \[ \begin{array}{ccl} S[i(t)] & = & \sqrt{2} \cdot I \cdot \cos(\omega \cdot t + \alpha) \\ & = & \underline{I} \end{array} \]
Definizione - Impedenza
L'impedenza \( \underline{Z}\) è una grandezza fisica (misurata in Ohm \( \mathrm{ \, \Omega }\)) associata a componenti in reti a regime sinusoidale e rappresentabile da un fasore.
Considerando la 1° legge di Ohm simbolica, ovvero \[ \underline{V} = \underline{Z} \cdot \underline{I} \] si ha che essa è definita come \[ \underline{Z} = \frac{\underline{V}}{\underline{I}} \] La fase di tale fasore indica lo sfasamento \( \varphi\) tra tensione e corrente:
Considerando la 1° legge di Ohm simbolica, ovvero \[ \underline{V} = \underline{Z} \cdot \underline{I} \] si ha che essa è definita come \[ \underline{Z} = \frac{\underline{V}}{\underline{I}} \] La fase di tale fasore indica lo sfasamento \( \varphi\) tra tensione e corrente:
- se tale valore è positivo, allora la tensione è in anticipo rispetto alla corrente;
- se tale valore è negativo, allora la tensione è in ritardo rispetto alla corrente.
Nota bene - Ad esempio
Considerando che la tensione simbolica e la corrente simbolica in una rete siano uguali a \[ \left\{ \begin{array}{ccl} \underline{V} & = & V \cdot \mathrm{e}^{\jmath \cdot \alpha} \\ \underline{I} & = & I \cdot \mathrm{e}^{\jmath \cdot \beta} \end{array} \right. \] si ha che è possibile calcolare l'impedenza come \[ \begin{array}{ccl} \underline{Z} & = & \frac{\underline{V}}{\underline{I}} \\ & = & \frac{V \cdot \mathrm{e}^{\jmath \cdot \alpha}}{I \cdot \mathrm{e}^{\jmath \cdot \beta}} \\ & = & \frac{V}{I} \cdot \mathrm{e}^{\jmath \cdot (\alpha - \beta)} \end{array} \]
Definizione - Ammettenza
È possibile definire l'ammettenza \( \underline{Y}\) (misurata in Siemens \( \mathrm{ \, S }\)) come il reciproco dell'impedenza \[ \underline{Y} = \; {}^{1} /_{\underline{Z}\;} \]
Definizione - Resistori in regime sinusoidale
Considerando un resistore in un circuito in regime sinusoidale, si ha che applicando la trasformata di Steinmetz all'equazione costitutiva di questo componente si ottiene \[ \begin{array}{ccl} v(t) = R \cdot i(t) & \xrightarrow{S[]} & S[v(t)] = S[R \cdot i(t)] \\ & \to & \underline{V} = R \cdot \underline{I} \end{array} \] Calcolando ora l'impedenza di tale componente, si ha che \[ \begin{array}{ccl} \underline{Z} & = & \frac{\underline{V}}{\underline{I}} \\ & = & R \end{array} \] ovvero, l'impedenza è un numero complesso (puramente reale) uguale a \[ \left\{ \begin{array}{ccl} Z_R & = & R \\ Z_I & = & 0 \end{array} \right. \quad \text{e} \quad \left\{ \begin{array}{ccl} \left| \underline{Z} \right| & = & R \\ \varphi & = & 0 \end{array} \right. \] È ora possibile graficare tale relazione (ipotizzando \( \alpha_V = 0\)) nel dominio fasoriale come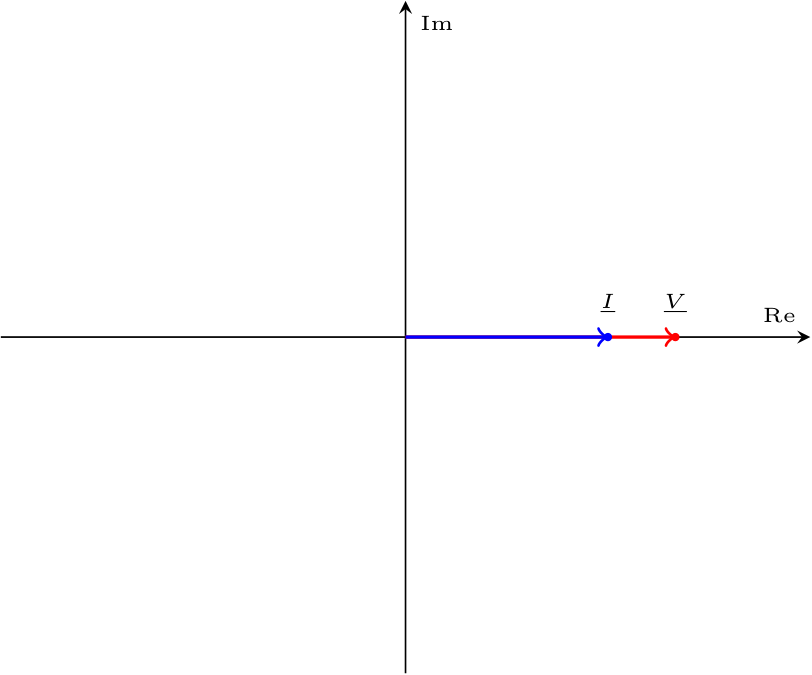 
e nel dominio temporale come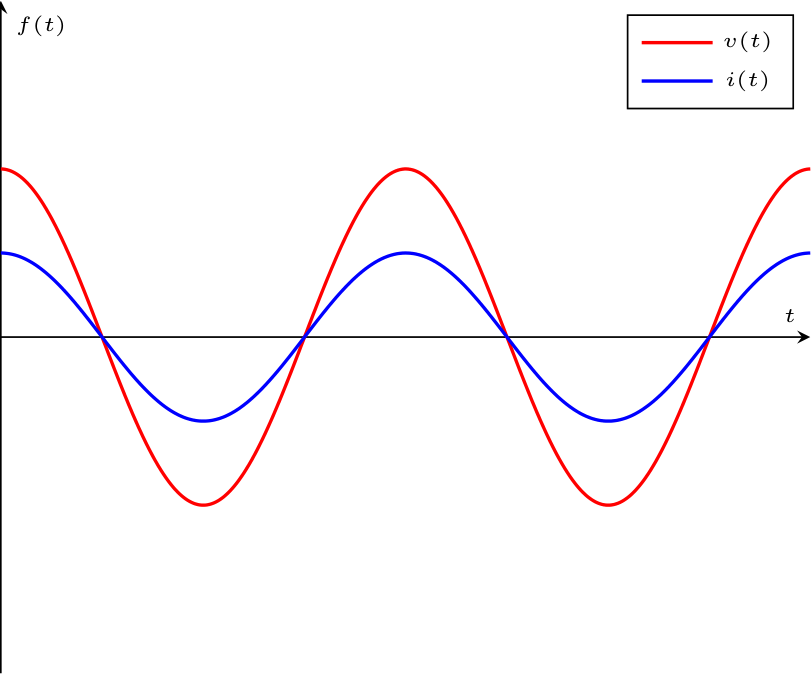 
Definizione - Induttori in regime sinusoidale
Considerando un induttore in un circuito in regime sinusoidale, si ha che applicando la trasformata di Steinmetz all'equazione costitutiva di questo componente si ottiene \[ \begin{array}{ccl} v(t) = L \cdot \frac{d}{d t} i(t) & \xrightarrow{S[]} & S[v(t)] = S\left[L \cdot \frac{d}{d t} i(t)\right] \\ & \to & \underline{V} = L \cdot S\left[\frac{d}{d t} i(t)\right] \\ & \to & \underline{V} = L \cdot \jmath \cdot \omega \cdot \underline{I} \end{array} \] Calcolando ora l'impedenza di tale componente, si ha che \[ \begin{array}{ccl} \underline{Z} & = & \frac{\underline{V}}{\underline{I}} \\ & = & \jmath \cdot \omega \cdot L \end{array} \] ovvero, l'impedenza è un numero complesso (puramente immaginario) uguale a \[ \left\{ \begin{array}{ccl} Z_R & = & 0 \\ Z_I & = & L \cdot \omega \end{array} \right. \quad \text{e} \quad \left\{ \begin{array}{ccl} \left| \underline{Z} \right| & = & L \cdot \omega \\ \varphi & = & \frac{\pi}{2} \end{array} \right. \] Ipotizzando la fase relativa alla tensione \( \alpha_V = 0\), si ha che è possibile calcolare la fase relativa alla corrente come \[ \begin{array}{ccl} \varphi = \alpha_V - \alpha_I & \to & \alpha_I = \alpha_V - \varphi \\ & \to & \alpha_I = 0 - \frac{\pi}{2} \\ & \to & \alpha_I = -\frac{\pi}{2} \end{array} \] È ora possibile graficare tale relazione nel dominio fasoriale come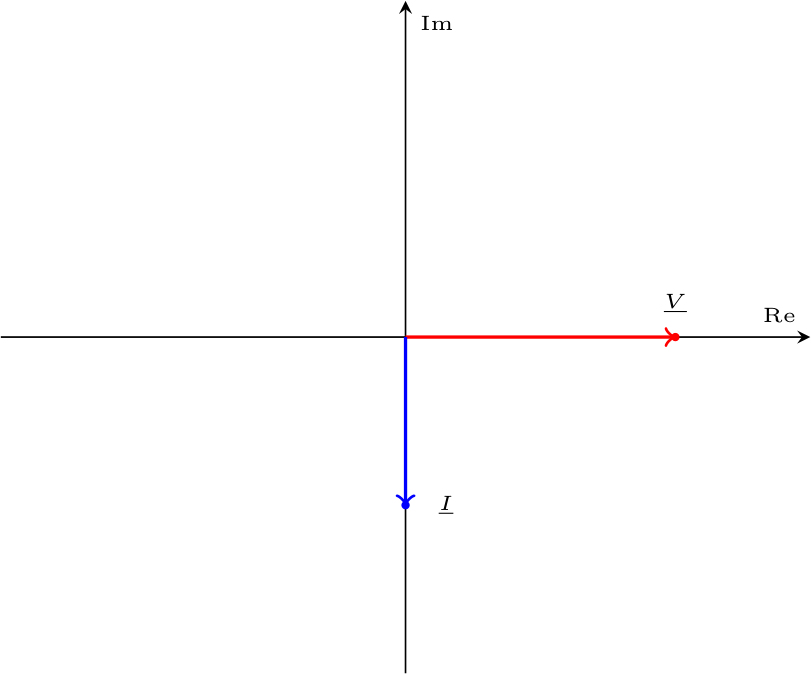 
e nel dominio temporale come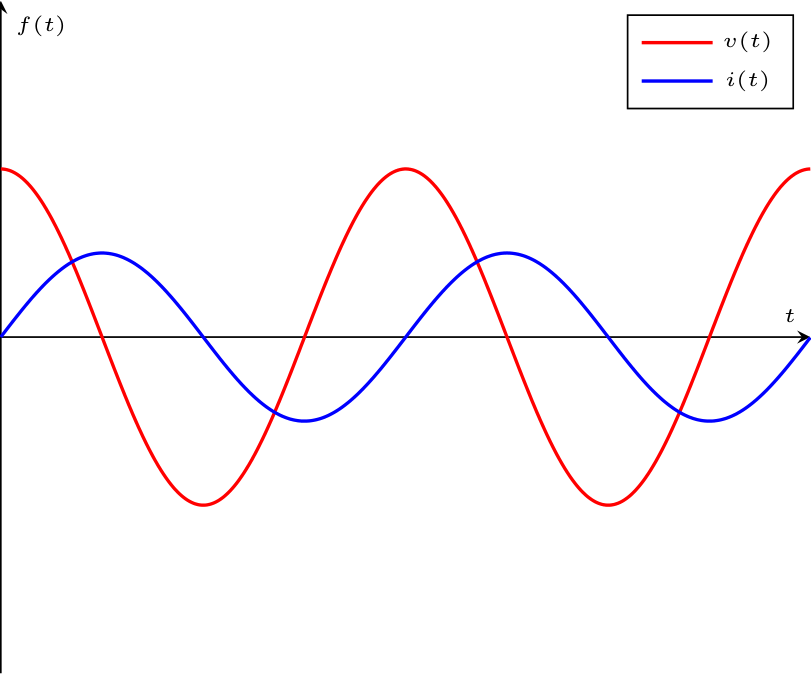 
Definizione - Condensatori in regime sinusoidale
Considerando un condensatore in un circuito in regime sinusoidale, si ha che applicando la trasformata di Steinmetz all'equazione costitutiva di questo componente si ottiene \[ \begin{array}{ccl} i(t) = C \cdot \frac{d}{d t} v(t) & \xrightarrow{S[]} & S[i(t)] = S\left[C \cdot \frac{d}{d t} v(t)\right] \\ & \to & \underline{I} = C \cdot S\left[\frac{d}{d t} v(t)\right] \\ & \to & \underline{I} = C \cdot \jmath \cdot \omega \cdot \underline{V} \end{array} \] Calcolando ora l'impedenza di tale componente, si ha che \[ \begin{array}{ccl} \underline{Z} & = & \frac{\underline{V}}{\underline{I}} \\ & = & \frac{1}{C \cdot \jmath \cdot \omega} \\ & \overset{\cdot \frac{\jmath}{\jmath}}{=} & \frac{1}{C \cdot \jmath \cdot \omega} \cdot \frac{\jmath}{\jmath} \\ & = & \jmath \cdot \left( -\frac{1}{C \cdot \omega} \right) \end{array} \] ovvero, l'impedenza è un numero complesso (puramente immaginario) uguale a \[ \left\{ \begin{array}{ccl} Z_R & = & 0 \\ Z_I & = & -\frac{1}{C \cdot \omega} \end{array} \right. \quad \text{e} \quad \left\{ \begin{array}{ccl} \left| \underline{Z} \right| & = & \frac{1}{C \cdot \omega}\\ \varphi & = & -\frac{\pi}{2} \end{array} \right. \] Ipotizzando la fase relativa alla corrente \( \alpha_V = 0\), si ha che è possibile calcolare la fase relativa alla corrente come \[ \begin{array}{ccl} \varphi = \alpha_V - \alpha_I & \to & \alpha_I = \alpha_V - \varphi \\ & \to & \alpha_I = 0 - \left( -\frac{\pi}{2} \right) \\ & \to & \alpha_I = \frac{\pi}{2} \end{array} \] È ora possibile graficare tale relazione nel dominio fasoriale come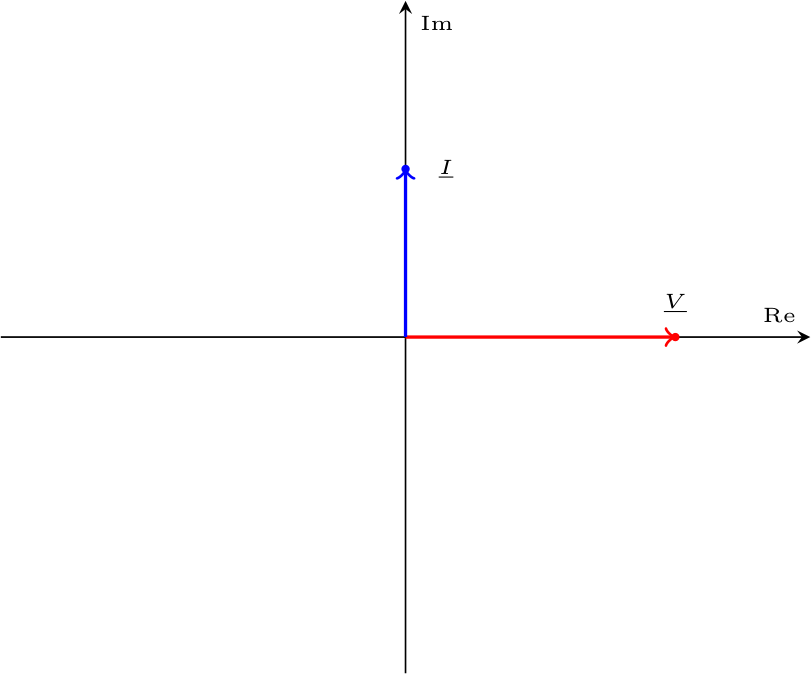 
e nel dominio temporale come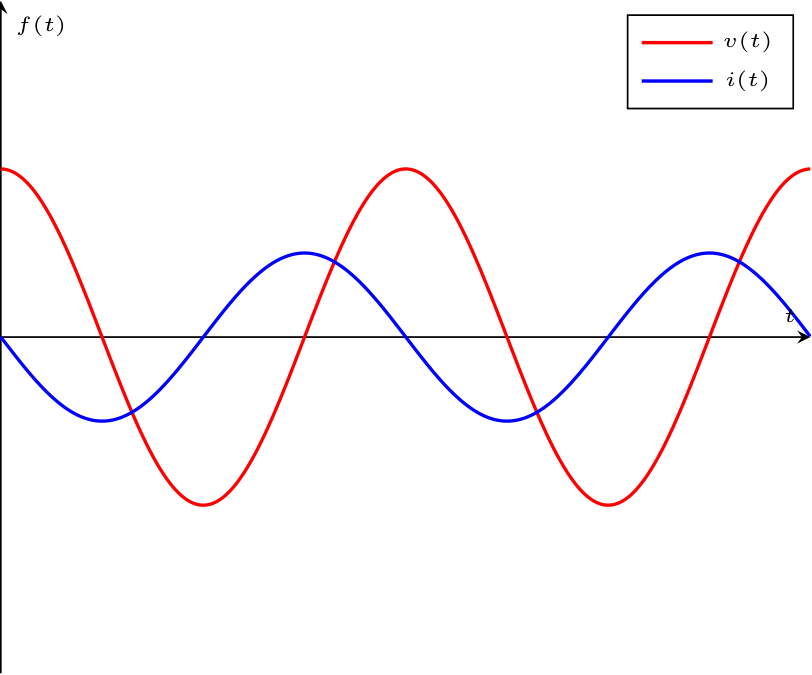 
Definizione - Reattanza
Considerando il fatto che l'impedenza è un numero complesso composto da una parte reale \( Z_R\) e una parte immaginaria \( Z_I\), ovvero \[ \underline{Z} = Z_R + \jmath \cdot Z_I \] e che una certa impedenza è introdotta dai diversi componenti passivi, ovvero
In particolare:
- nel caso di resistori con resistenza \( R\), è introdotta un'impedenza uguale a \[ \left\{ \begin{array}{ccl} Z_R & = & R \\ Z_I & = & 0 \end{array} \right. \]
- nel caso di induttori con induttanze \( L\), è introdotta un'impedenza uguale a \[ \left\{ \begin{array}{ccl} Z_R & = & 0 \\ Z_I & = & \omega \cdot L \end{array} \right. \]
- nel caso di condensatori di capacità \( C\), è introdotta un'impedenza uguale a \[ \left\{ \begin{array}{ccl} Z_R & = & 0 \\ Z_I & = & -\frac{1}{\omega \cdot C} \end{array} \right. \]
In particolare:
- nel caso di circuiti RL, si ha una reattanza induttiva \( X_L\) dove \[ X_L = \omega \cdot L \]
- nel caso di circuiti RC, si ha una reattanza capacitiva \( X_C\) dove \[ X_C = -\frac{1}{\omega \cdot C} \]
Dimostrazione - Impedenze in serie e impedenza equivalente
Data la proposizione
Enunciato:
Date \( n\) impedenze poste in serie (ovvero che condividono la stessa corrente)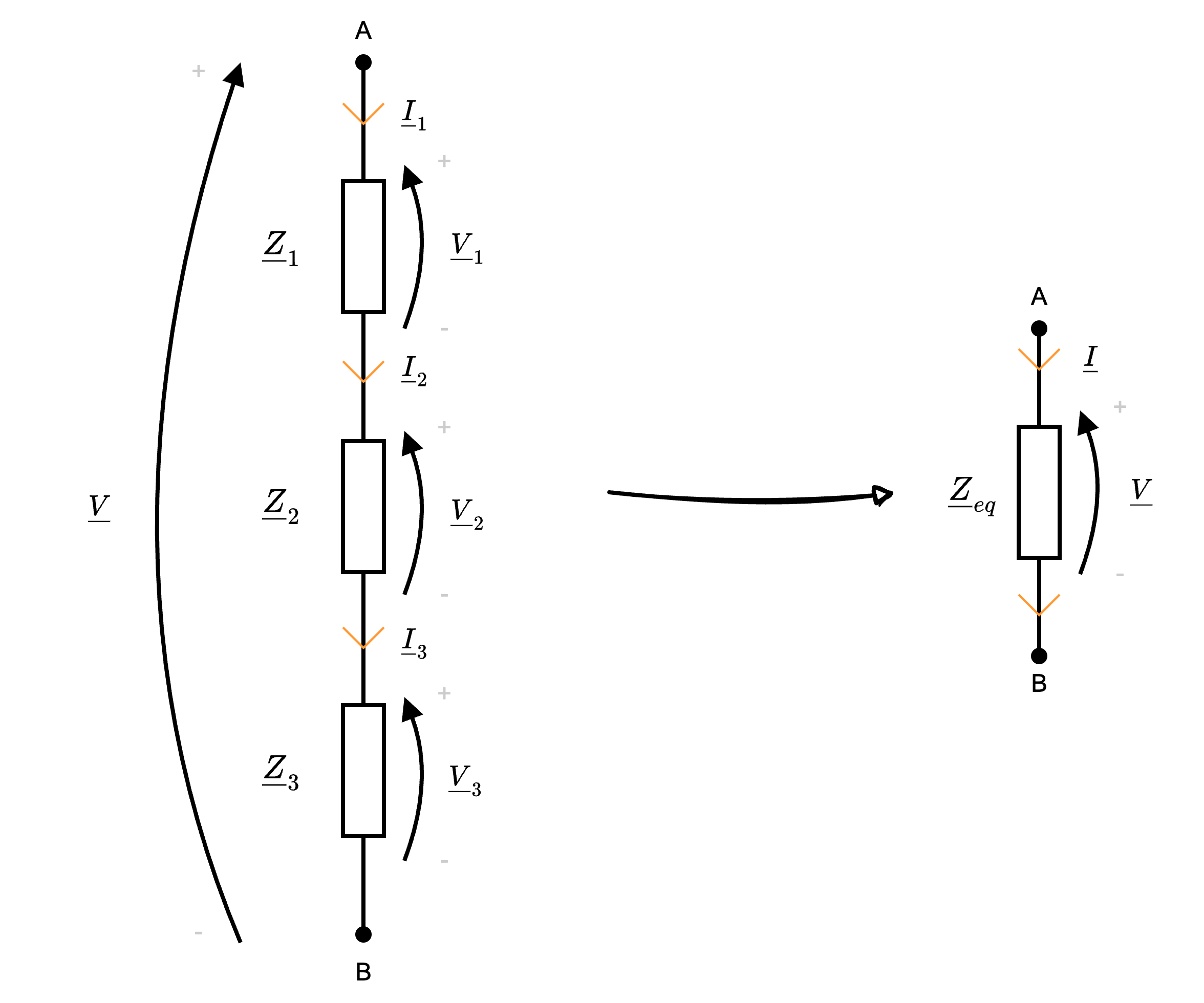 
si ha che è possibile sostituirle con un'unica impedenza, il cui valore è uguale a \[ \underline{Z}_{eq} = \sum_{j = 1}^{n} \underline{Z}_j \]
Dimostrazione:
Per dimostrare questa proposizione consideriamo il caso di 3 impedenze in serie (poi facilmente generalizzabile).
Ipotizziamo che tali impedenze appartengano ad una "maglia chiusa"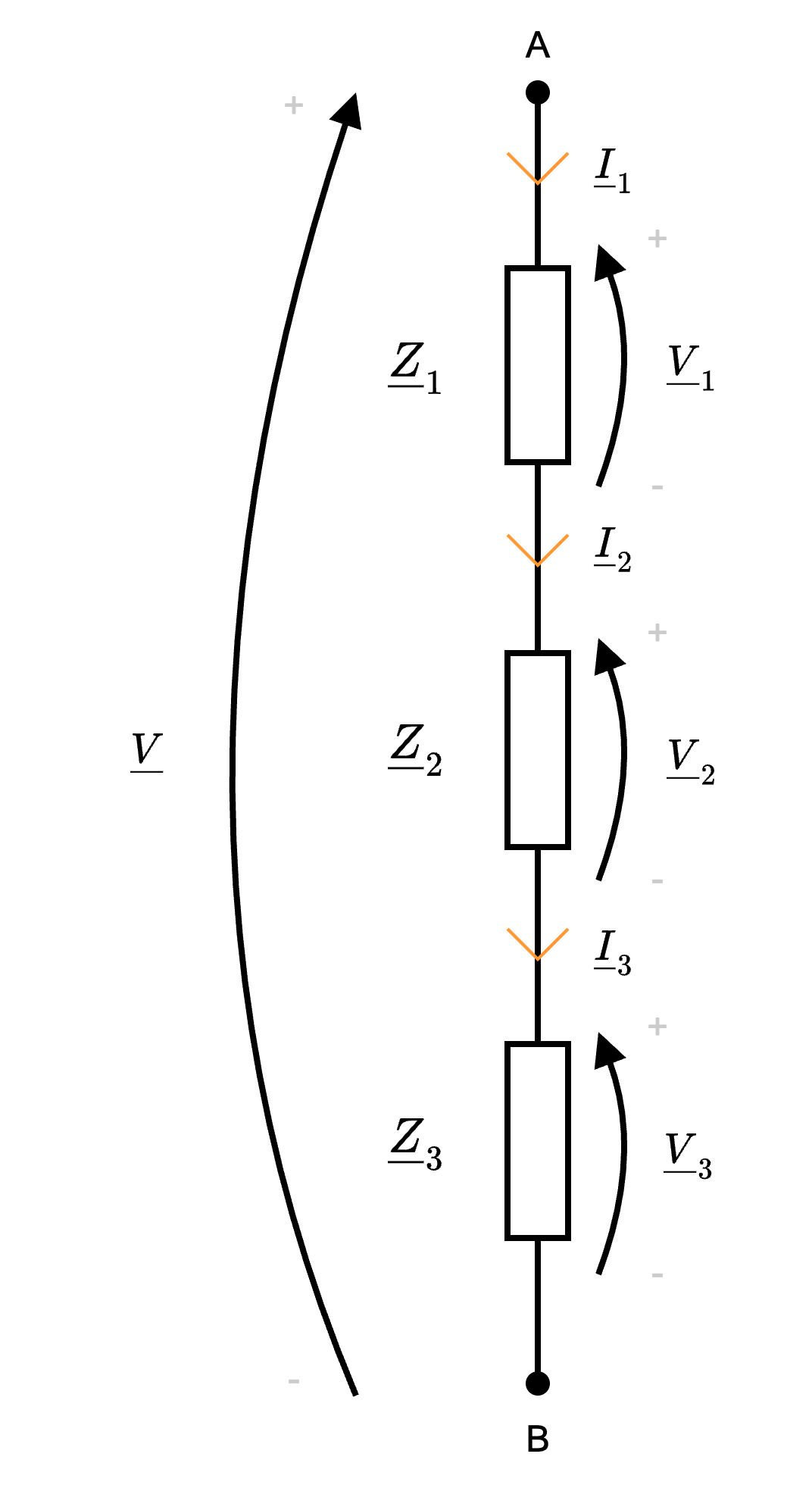
è quindi possibile applicare LKT, da cui si ottiene \[ \underline{V} - \underline{V}_1 - \underline{V}_2 - \underline{V}_3 = 0 \] da cui \[ \begin{array}{ccl} \underline{V} & = & \underline{V}_1 - \underline{V}_2 - \underline{V}_3 \\ & \overbrace{=}^{\text{eq. cost.}} & \underline{Z}_1 \cdot \underline{I}_1 + \underline{Z}_2 \cdot \underline{I}_2 + \underline{Z}_3 \cdot \underline{I}_3 \\ & \overbrace{=}^{\underline{I}_1 = \underline{I}_2 = \underline{I}_3 = \underline{I}} & (\underline{Z}_1 + \underline{Z}_2 + \underline{Z}_3) \cdot \underline{I} \\ & = & \underline{Z}_{eq} \cdot \underline{I} \end{array} \] dove \[ \underline{Z}_{eq} = \underline{Z}_1 + \underline{Z}_2 + \underline{Z}_3 \] Generalizzando questo risultato a \( n\) impedenze in serie, si è dimostrata la proposizione.
Ipotizziamo che tali impedenze appartengano ad una "maglia chiusa"
Dimostrazione - Impedenze in parallelo e impedenza equivalente
Data la proposizione
Enunciato:
Date \( n\) impedenze poste in parallelo (ovvero che hanno la stessa tensione o sono collegati agli stessi nodi)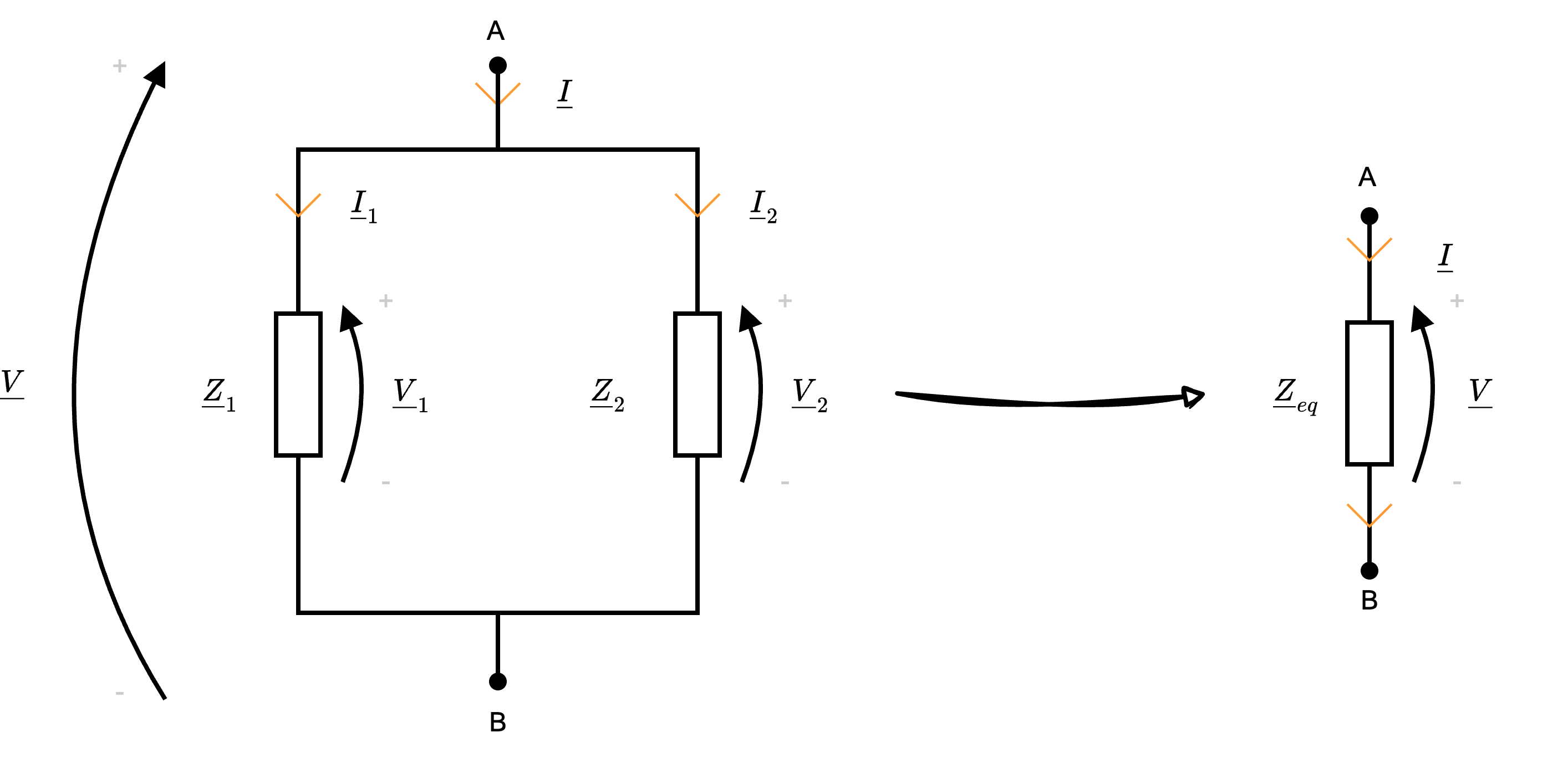 
si ha che è possibile sostituirli con un'unica impedenza, il cui valore è uguale a \[ \underline{Z}_{eq} = \left( \sum_{j = 1}^{n} \frac{1}{\underline{Z}_j} \right)^{-1} \]
Dimostrazione:
Per dimostrare questa proposizione consideriamo il caso di 2 rami in parallelo (poi facilmente generalizzabile).
Ipotizziamo che tali impedenze appartengano ad una "superficie chiusa"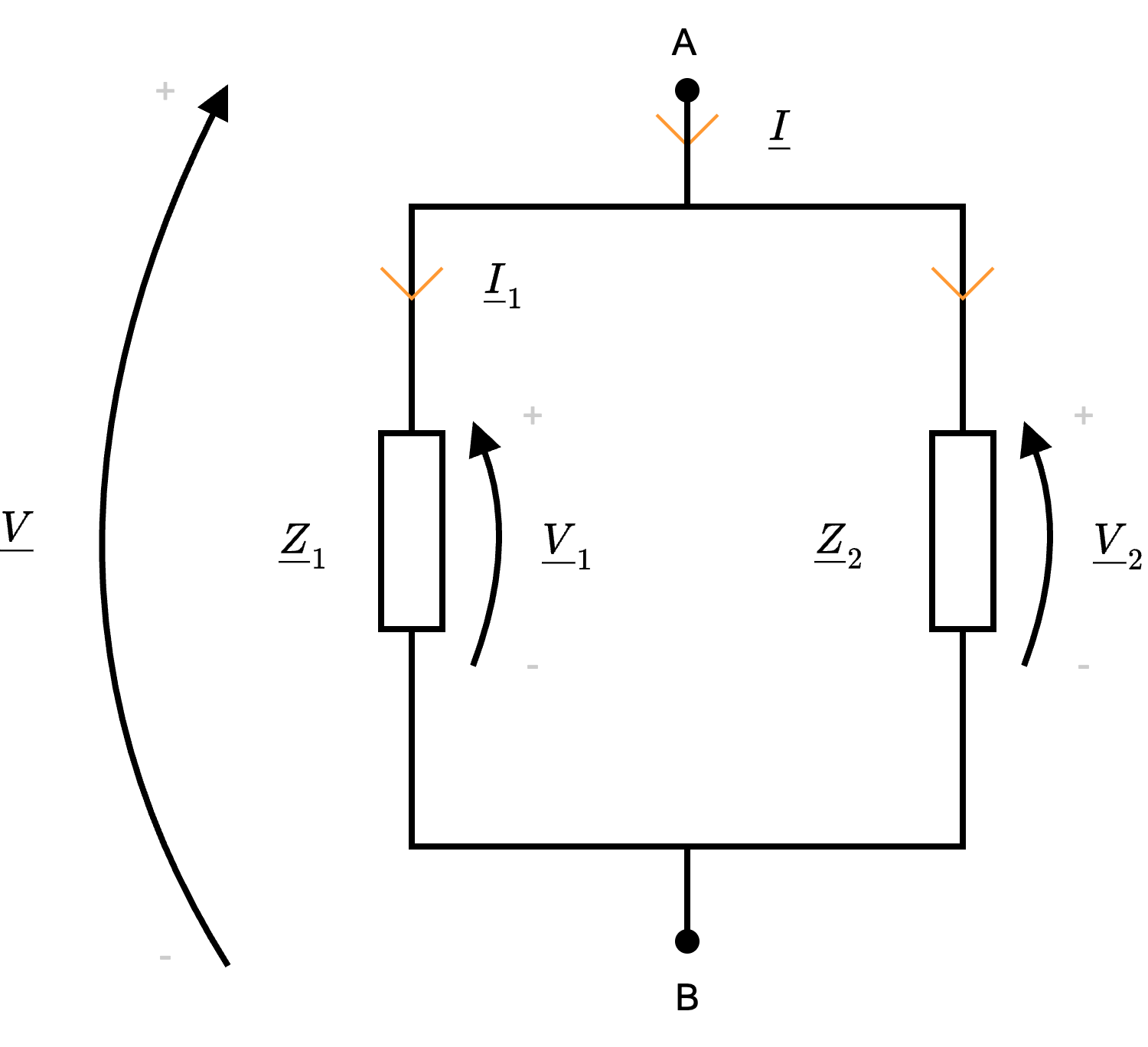
è quindi possibile applicare LKC, da cui si ottiene \[ \underline{I} - \underline{I}_1 - \underline{I}_2 = 0 \] da cui \[ \begin{array}{ccl} \underline{I} & = & \underline{I}_1 + \underline{I}_2 \\ & \overbrace{=}^{\text{eq. cost.}} & \frac{\underline{V}_1}{\underline{Z}_1} + \frac{\underline{V}_2}{\underline{Z}_2} \\ & \overbrace{=}^{\underline{V}_1 = \underline{V}_2 = \underline{V}} & \frac{\underline{V}}{\underline{Z}_1} + \frac{\underline{V}}{\underline{Z}_2} \\ & = & \underline{V} \cdot \underbrace{\left( \frac{1}{\underline{Z}_1} + \frac{1}{\underline{Z}_2} \right)}_{\text{ammettenza equiv.}} \\ & = & \underline{V} \cdot \underline{Y}_{eq} \end{array} \] dove \( Y_{eq}\) è l'ammettenza equivalente ed è uguale a \[ \underline{Y}_{eq} = \frac{1}{\underline{Z}_1} + \frac{1}{\underline{Z}_2} \] Ricordando che \[ \underline{Z}_{eq} = \frac{1}{\underline{Y}_{eq}} \] si ha che generalizzando questo risultato a \( n\) impedenze in parallelo, si è dimostrata la proposizione.
Ipotizziamo che tali impedenze appartengano ad una "superficie chiusa"
Nota bene - Formula per il caso \( n = 2\)
Considerando il caso \( n = 2\), si ha che l'ammettanza equivalente è uguale a \[ \begin{array}{ccl} \underline{Y}_{eq} & = & \frac{1}{\underline{Z}_1} + \frac{1}{\underline{Z}_2} \\ & = & \frac{\underline{Z}_2 + \underline{Z}_1}{\underline{Z}_1 \cdot \underline{Z}_2} \end{array} \] da cui è poi semplice calcolare l'impedenza equivalente, uguale a \[ \begin{array}{ccl} \underline{Z}_{eq} & = & \frac{1}{\underline{Y}_{eq}} \\ & = & \frac{1}{\frac{\underline{Z}_2 + \underline{Z}_1}{\underline{Z}_1 \cdot \underline{Z}_2}} \\ & = & \frac{\underline{Z}_1 \cdot \underline{Z}_2}{\underline{Z}_2 + \underline{Z}_1} \end{array} \]
Esempio - Risoluzione di un circuito in regime sinusoidale
Considerando il seguente circuito in regime sinusoidale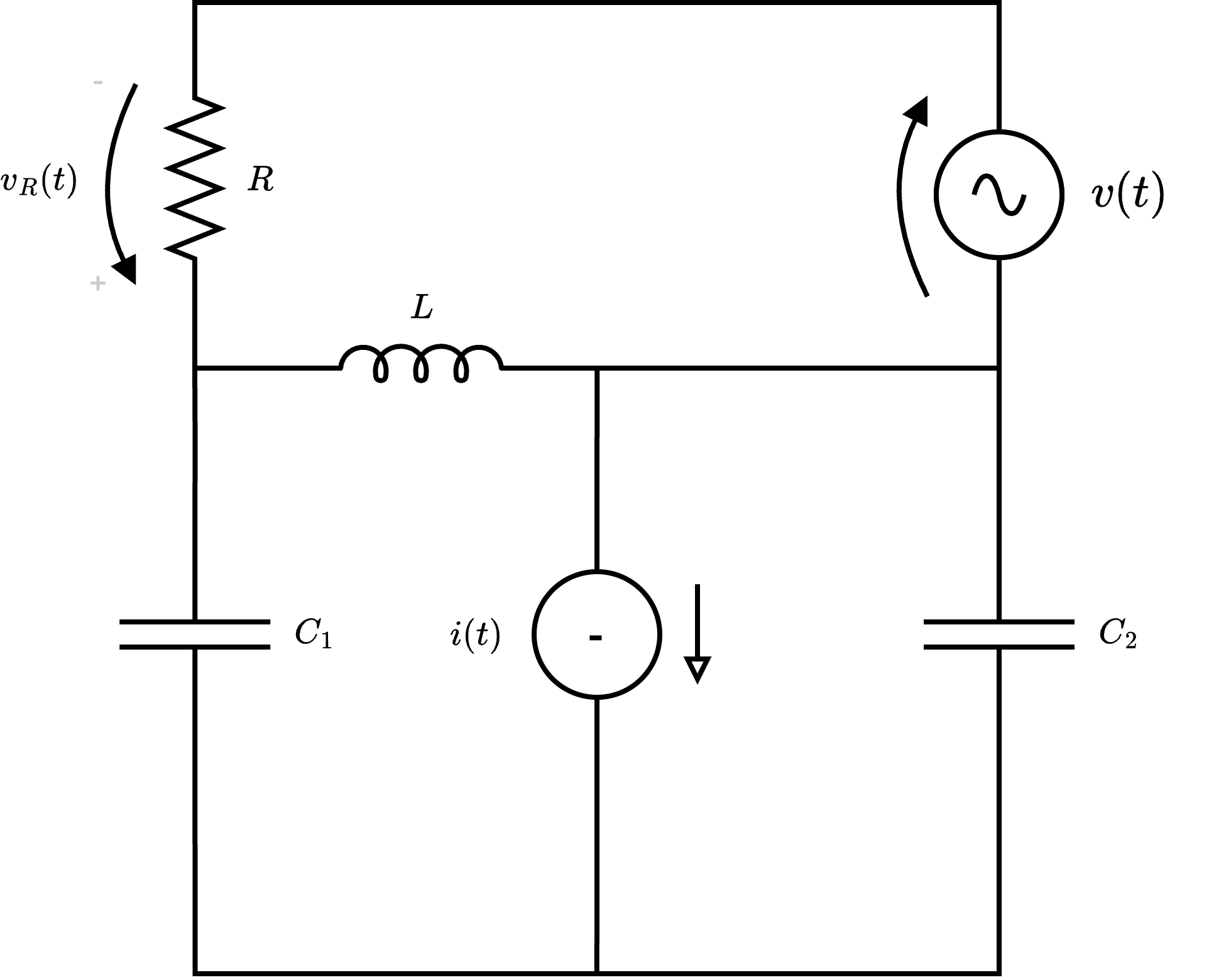 
dove \[ i(t) = \hat{I} \cdot \cos(\omega \cdot t + \alpha_I) \] e \[ v(t) = \hat{V} \cdot \sin\left( \omega \cdot t + \alpha_V \right) \] calcolare: Occorre ora calcolare i fasori e le impedenze del circuito: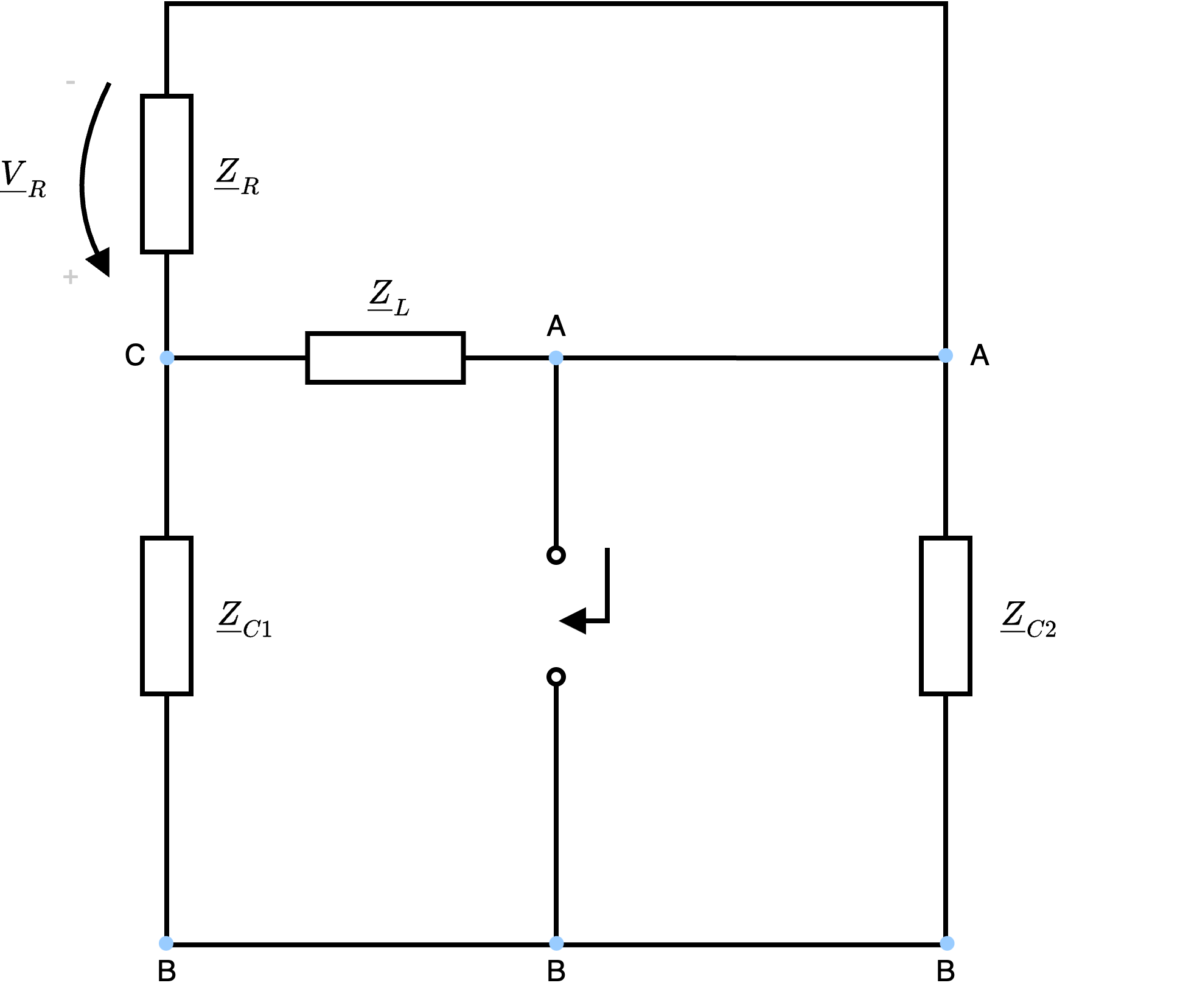 
È quindi possibile individuare che le impedenze \( \underline{Z}_R\) e \( \underline{Z}_L\) sono in parallelo ed è quindi possibile sostituirle con l'impedenza \( \underline{Z}_X\) \[ \underline{Z}_{X} = \underline{Z}_R \ // \ \underline{Z}_L \] 
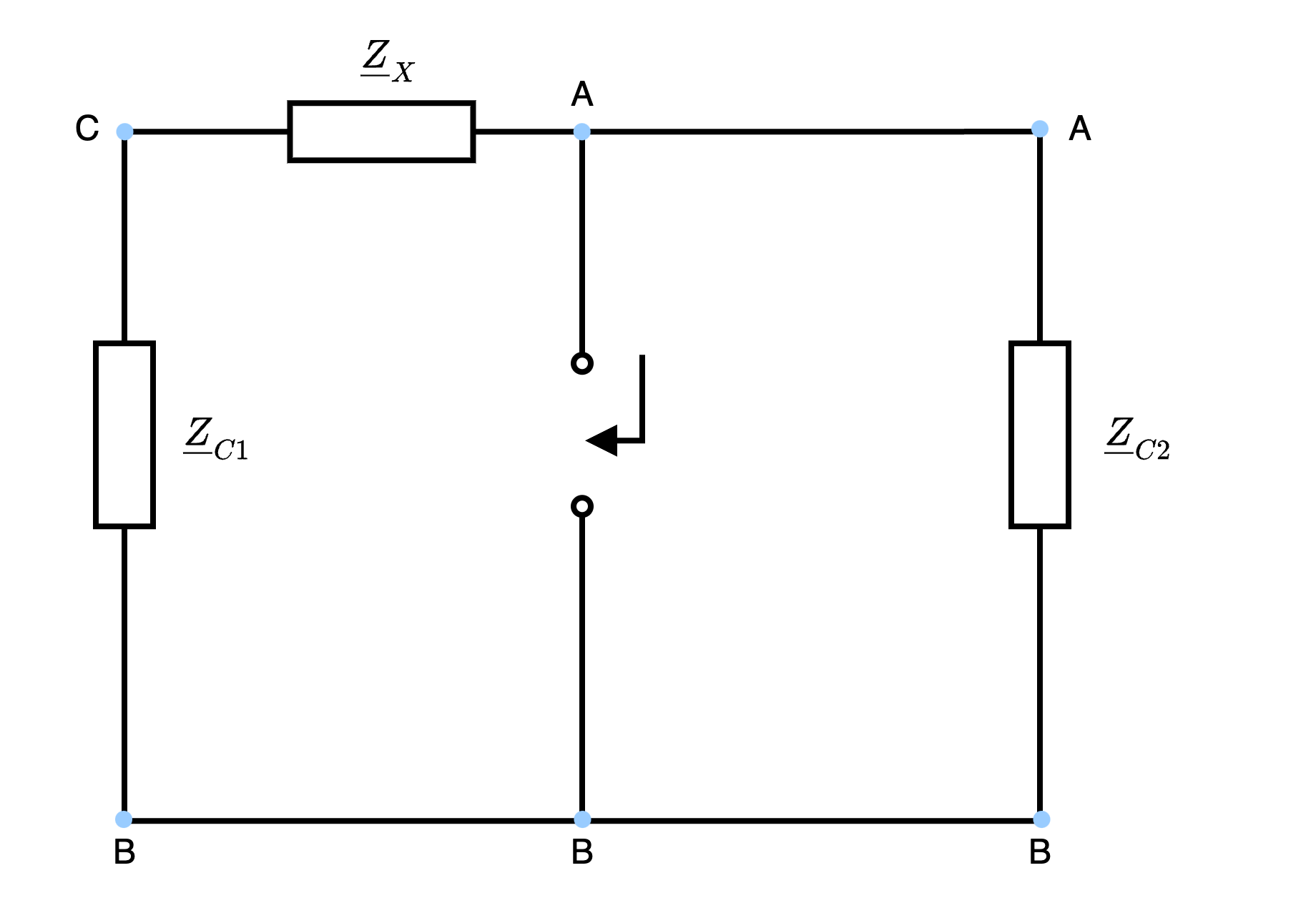È quindi possibile calcolare l'impedenza equivalente come \[ \begin{array}{ccl} \underline{Z}_{eq} & = & (\underline{Z}_X + \underline{Z}_{C1}) \ // \ \underline{Z}_{C2} \\ & = & [ (\underline{Z}_R // \underline{Z}_L ) + \underline{Z}_{C1} ] \ // \ \underline{Z}_{C2} \end{array} \]
- i fasori \( \underline{I}\) e \( \underline{V}\) e tutte le impedenze del circuito;
- l'impedenza equivalente \( \underline{Z}_{eq}\) del circuito vista dal generatore di corrente;
- il fasore \( \underline{V}_R\) e la funzione \( v_1(t)\).
Applicazione della trasformata di Steinmetz e calcolo di fasori e impedenze
Per risolvere questo esercizio, applichiamo la trasformata di Steinmetz al circuito, ottenendo- per calcolare il fasore \( \underline{I}\) consideriamo che la struttura generica di un fasore è la seguente \[ \underline{I} = I \cdot \mathrm{e}^{\jmath \cdot \alpha_I} \] dove \( I\) è il valore efficace. Per calcolare tale valore, è necessario considerare che \[ I = \frac{\hat{I}}{\sqrt{2}} \]
- per calcolare il fasore \( \underline{V}\), è necessario considerare di rendere uniforme la funzione trigonometrica utilizzata per descrivere il segnale. Dato che si vuole utilizzare il coseno, consideriamo che \[ \sin(\alpha) = \cos(\alpha - 90^\circ) \] e otteniamo la funzione \[ \begin{array}{ccl} v(t) & = & \hat{V} \cdot \cos(\omega \cdot t + \alpha_V - 90^\circ) \\ & = & \hat{V} \cdot \cos(\omega \cdot t + \alpha_{V}') \end{array} \] Considerando ora che \[ V = \frac{\hat{V}}{\sqrt{2}} \] si ha che è possibile calcolare il fasore \( \underline{V}\) come \[ \underline{V} = V \cdot \mathrm{e}^{\jmath \cdot \alpha_V'} \]
- per l'impedenza \( \underline{Z}_R\) associata alla resistenza \( R\), è necessario calcolare \[ \underline{Z}_R = R \]
- per l'impedenza \( \underline{Z}_L\) associata all'induttore \( L\), è necessario calcolare \[ \underline{Z}_L = \jmath \cdot \omega \cdot L \]
- per calcolare l'impendenza \( \underline{Z}_{C1}\) associata al condensatore \( C_1\), è necessario calcolare \[ \underline{Z}_{C1} = \jmath \cdot \left( -\frac{1}{\omega \cdot C_1} \right) \]
- per calcolare l'impendenza \( \underline{Z}_{C2}\) associata al condensatore \( C_2\), è necessario calcolare \[ \underline{Z}_{C2} = \jmath \cdot \left( -\frac{1}{\omega \cdot C_2} \right) \]
Calcolo dell'impedenza equivalente vista dal generatore di corrente
Per calcolare l'impedenza equivalente del circuito vista dal generatore di corrente, è necessario passivare tutti i generatori. Si ha quindi il seguente circuitoCalcolo di \( \underline{V}_R\) e \( v_1(t)\)
Al fine di calcolare \( \underline{V}_R\), è possibile considerare di utilizzare il principio di sovrapposizione degli effetti per cui vale \[ \underline{V}_R = \underline{V}_R' + \underline{V}_R'' \]- per calcolare \( \underline{V}_R'\), consideriamo il circuito in cui è passivato il generatore di corrente Da questo, è possibile poi considerare che le impedenze \( \underline{Z}_{C1}\) e \( \underline{Z}_{C2}\) sono in serie e possono essere sostituite dall'impedenza \( Z_A'\) \[ \underline{Z}_A' = Z_{C1} + \underline{Z}_{C2} \]
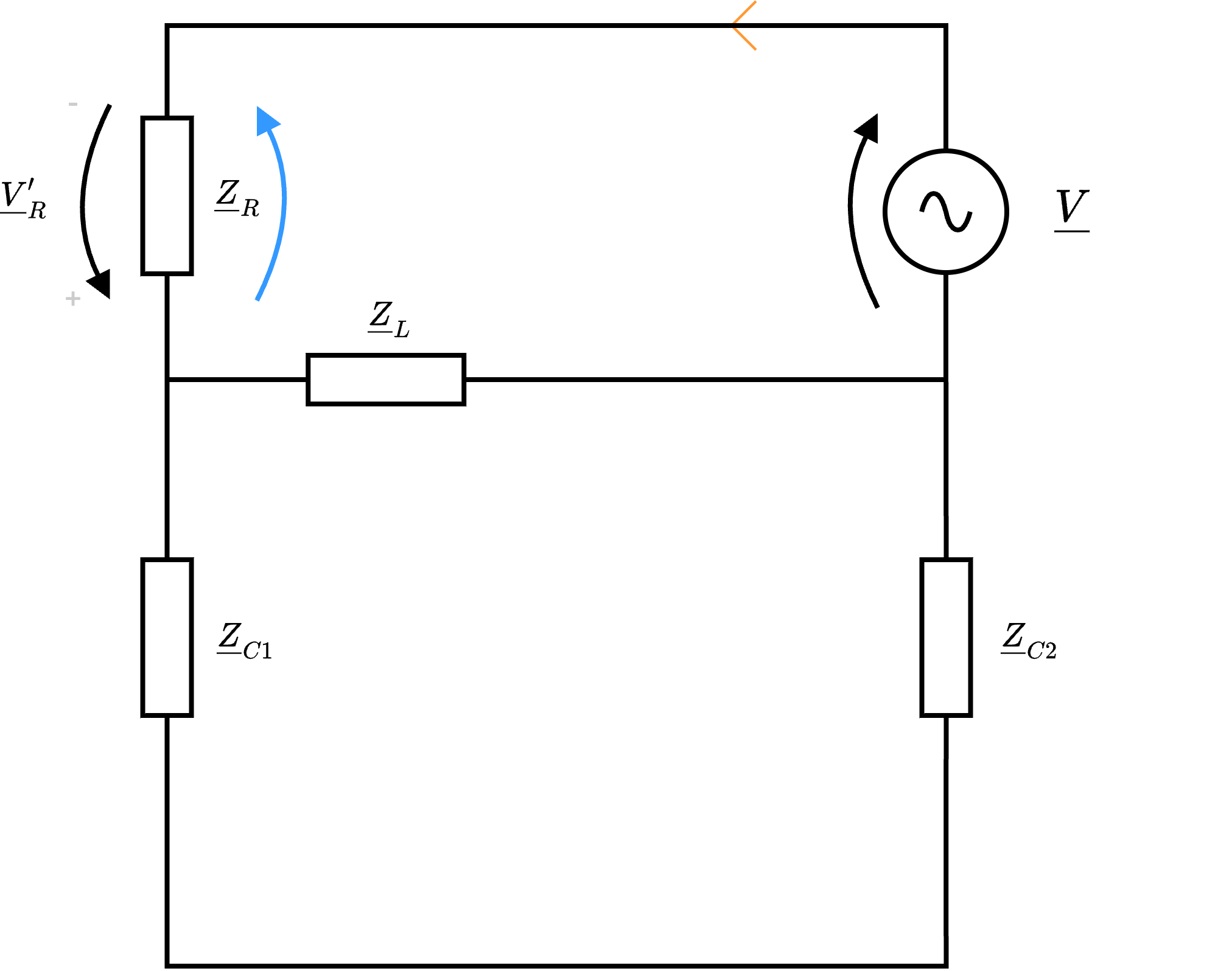A questo punto, è possibile considerare che le impedenze \( \underline{Z}_L\) e \( \underline{Z}_A'\) sono in parallelo ed è quindi possibile sostituirle con l'impedenza \( \underline{Z}_B'\) \[ \underline{Z}_B' = \underline{Z}_A' \ // \ Z_L \]
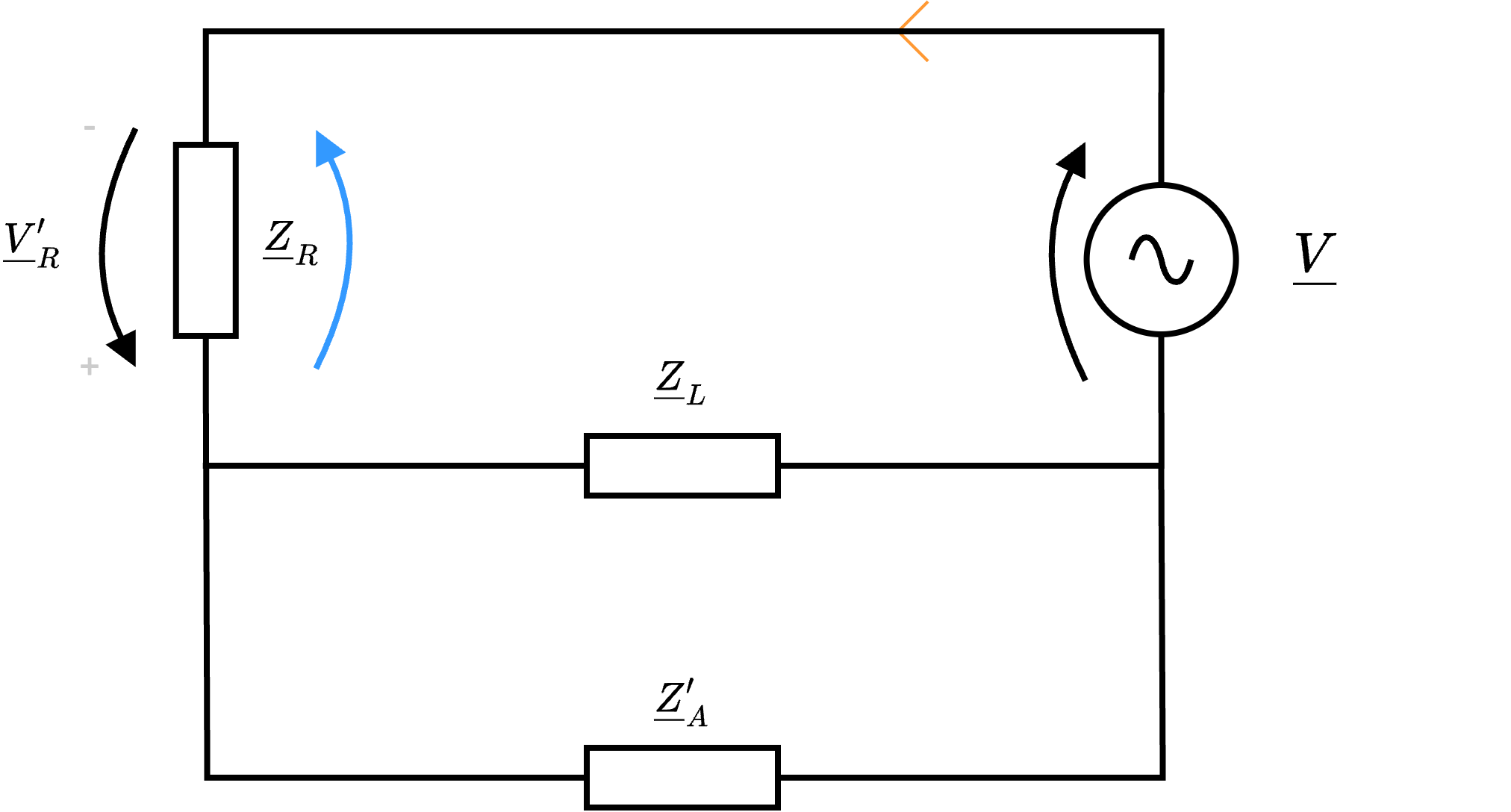È ora possibile calcolare \( \underline{V}_R'\) utilizzando il partitore di tensione \[ \underline{V}_R' = -\underline{V} \cdot \frac{\underline{Z}_R}{\underline{Z}_B' + \underline{Z}_R} \] (ndr, il segno è negativo perchè nel circuito iniziale si utilizza una convenzione contraria a quella del generatore); - per calcolare \( \underline{V}_R''\), consideriamo il circuito in cui è passivato il generatore di tensione È possibile semplificare il circuito sostituendo alle impedenze \( \underline{Z}_R\) e \( \underline{Z}_L\) in parallelo l'impedenza \( \underline{Z}_D''\) \[ \underline{Z}_D'' = \underline{Z}_L \ // \ \underline{Z}_R \]
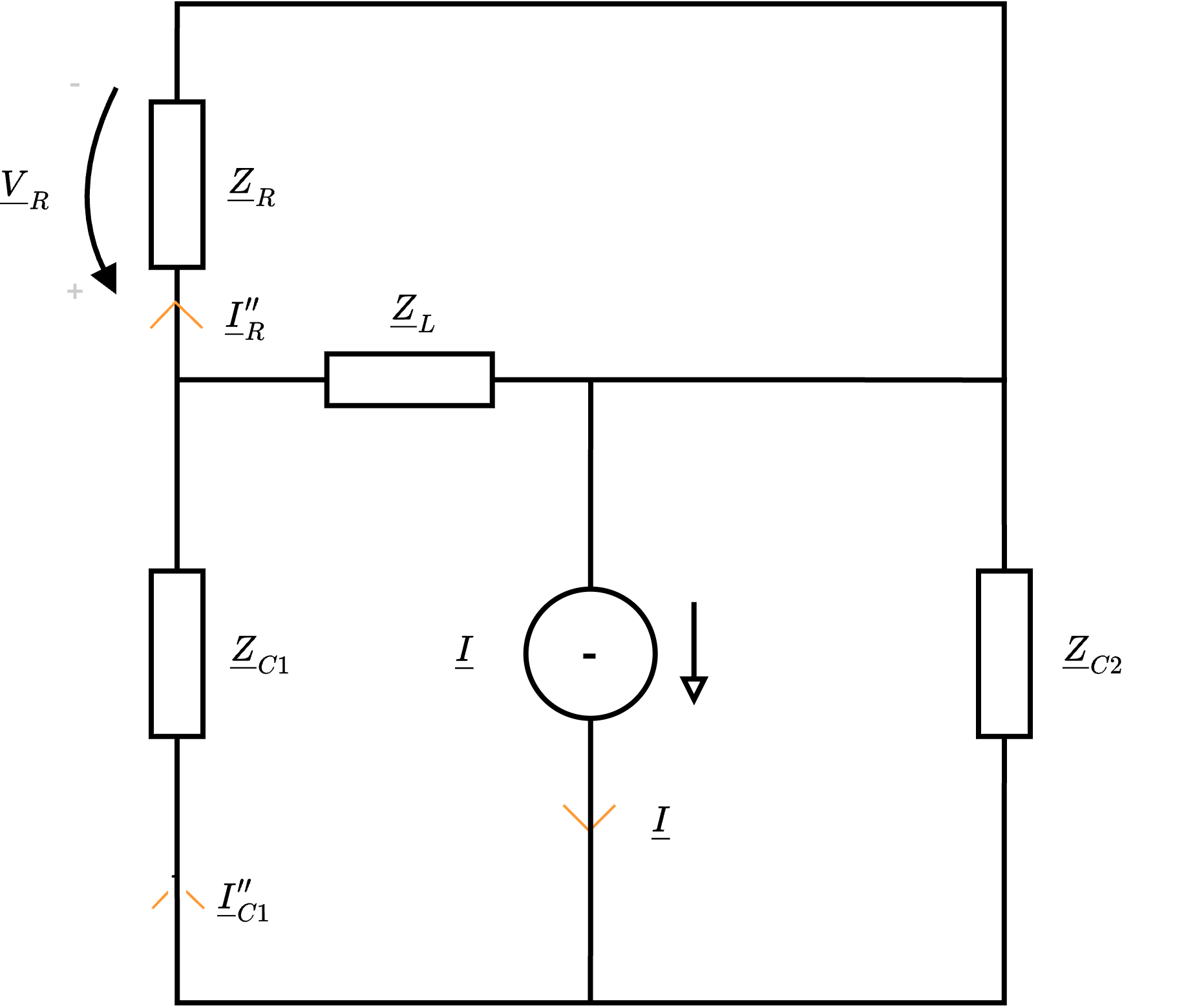e alle impedenze \( \underline{Z}_D''\) e \( \underline{Z}_{C1}\) in serie, l'impedenza \( \underline{Z}_{E}''\) \[ \underline{Z}_{E}'' = \underline{Z}_{D}'' + \underline{Z}_{C1} \]
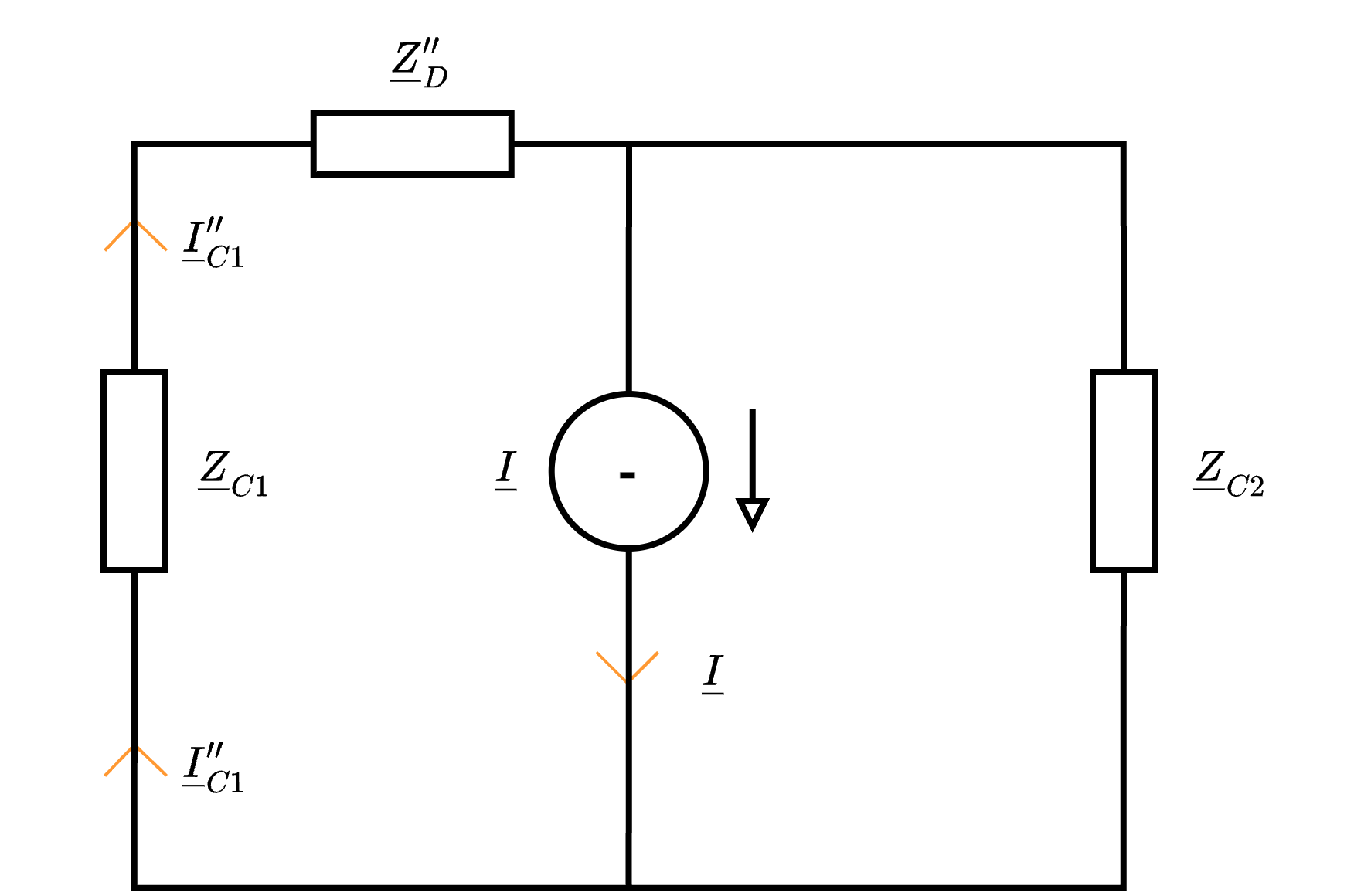Al fine di calcolare \( \underline{I}_C''\), è possibile utilizzare il partitore di corrente \[ \underline{I}_{C1}'' = \underline{I} \cdot \frac{\underline{Z}_E'' \ // \ \underline{Z}_{C2}}{\underline{Z}_E''} \] Considerando ora che la corrente è ripartita anche nel parallelo \( \underline{Z}_D''\), si ha che è possibile calcolare \[ \underline{I}_R'' = \underline{I}_{C2}'' \cdot \frac{\underline{Z}_D''}{\underline{Z}_{R}} \] Infine, è possibile considerare la legge di Ohm per calcolare \( \underline{V}_R''\), ovvero \[ \underline{V}_R'' = \underline{I}_R'' \cdot \underline{Z}_R \]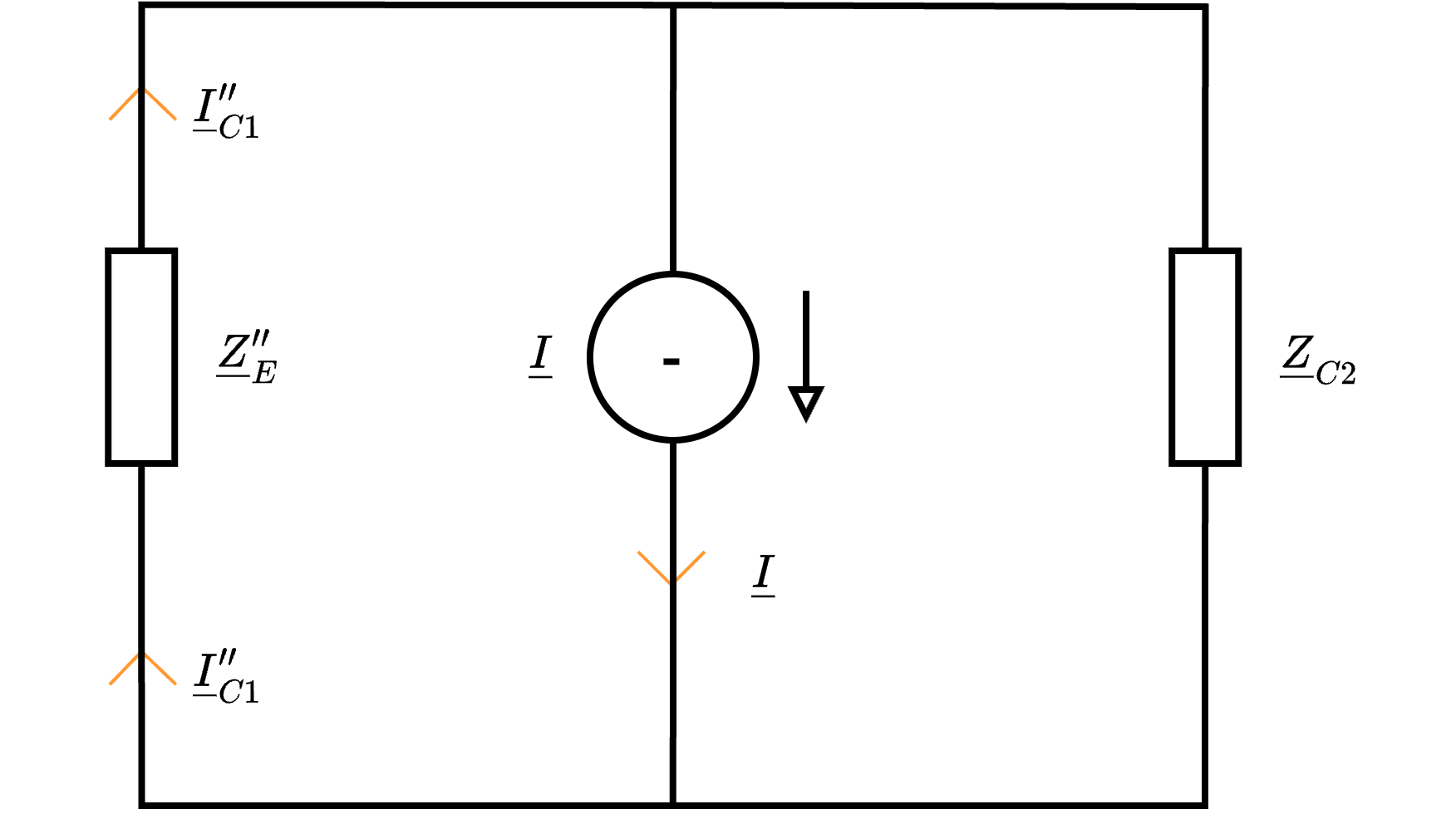
- \( \hat{V}_R\) è il valore di picco ed è uguale a \[ \hat{V}_R = \sqrt{2} \cdot \left| \underline{V}_R \right| \]
- \( \alpha_{VR}\) è l'argomento di \( \underline{V}_R\).