Definizione - Interruttore
Un interruttore è un componente che può cambiare ad un certo istante \( t\) la topologia del circuito.
Tale componente può essere sia aperto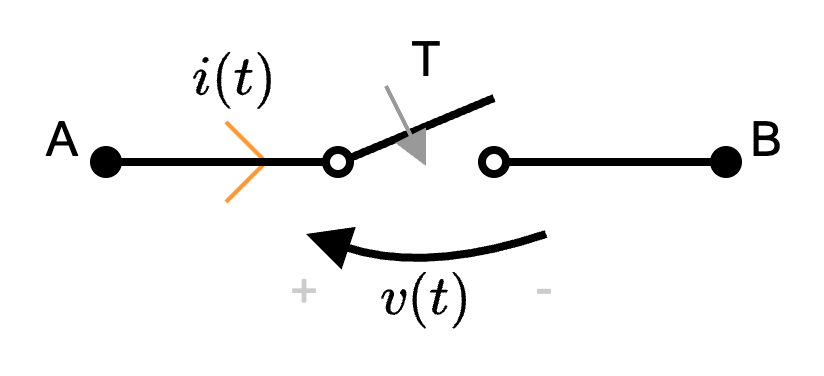
rendendo il circuito aperto che chiuso 
determinando un cortocircuito.
Tale componente può essere sia aperto
Definizione - Transitorio
Un transitorio è un cambio di stato energetico e può avvenire per:
- generatori variabili (ad esempio, generatori a gradino);
- guasti;
- cambio di stato di interruttori.
Dimostrazione - Circuiti RC
Data la proposizione
Enunciato:
Considerando un circuito RC (formato da una resistenza \( R\) e un Condensatore \( C\))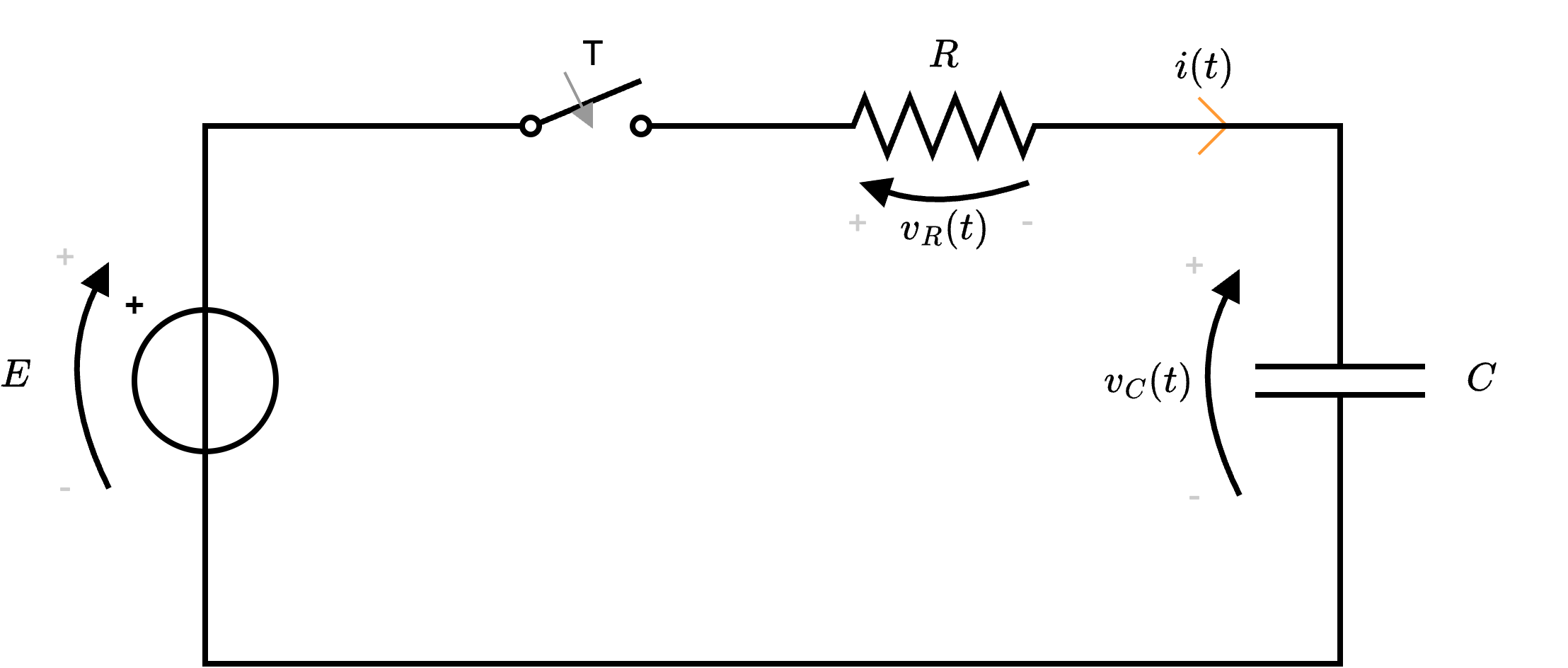 
sotto le seguenti ipotesi:
Si definisce infatti la tensione \[ v_C(t) = \underbrace{(v_{C0} - E) \cdot \mathrm{e}^{-\frac{t}{\tau}}}_{\text{Risp. transitoria}} + \underbrace{E}_{\text{Risp. a regime}} \] divisa in: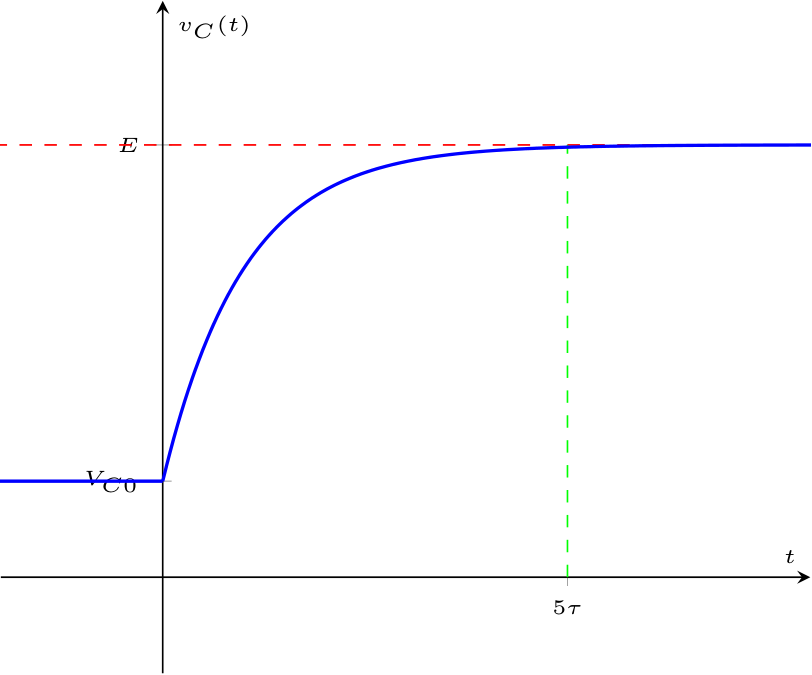
In maniera analoga, è possibile vedere la funzione \[ v_C(t) = \underbrace{v_{C0} \cdot \mathrm{e}^{-\frac{t}{\tau}}}_{\text{evoluzione libera}} + \underbrace{E \cdot \left( 1 - \mathrm{e}^{-\frac{t}{\tau}} \right)}_{\text{risposta forzata}} \] divisa in: 
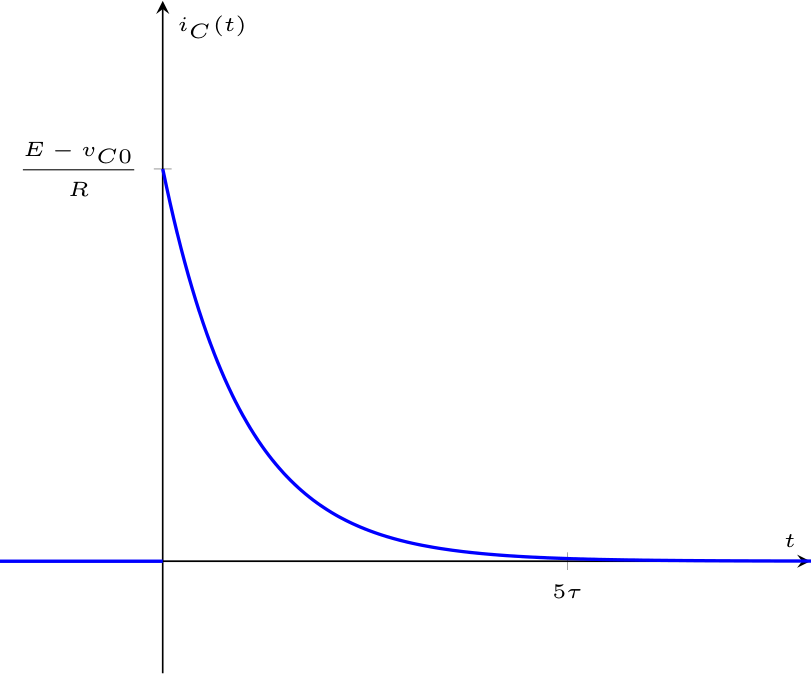Come è evidente dal grafico, la corrente varia istantaneamente partendo dal valore nullo (a causa del circuito aperto) per poi raggiungere il massimo istantaneamente e infine decrescere.
- il condensatore inizialmente ha una certa energia \( v_{C0}\), ovvero la tensione iniziale (all'istante \( t_0 = 0^-\)) del condensatore è uguale a \( v_{C0}\), cioè \[ v(t_0 = 0^-) = v_{C0} \]
- all'istante \( t_1 = 0 \mathrm{ \, s }\), l'interruttore T si chiude.
Tensione ai capi del condensatore
La tensione ai capi del condensatore \( v_C(t)\) ha il seguente comportamento \[ v_C(t) = (v_{C0} - E) \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} + E \]Costante di tempo del sistema
È possibile definire la costante di tempo del sistema \( \tau\) (misurata in secondi \( \mathrm{ \, s }\)) che informa del tempo di risposta del circuito: \[ \tau = R \cdot C \] È quindi possibile riscrivere la funzione \( v_C(t)\) come \[ v_C(t) = (v_{C0} - E) \cdot \mathrm{e}^{-\frac{t}{\tau}} + E \]Corrente del circuito
La corrente \( i_C(t)\) ha il seguente comportamento \[ i_C(t) = \frac{E - v_{C0}}{R} \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} \]Interpretazione delle funzioni
È possibile interpretare la funzione \( v_C(t)\) al fine di capire l'evoluzione dell'energia del condensatore.Si definisce infatti la tensione \[ v_C(t) = \underbrace{(v_{C0} - E) \cdot \mathrm{e}^{-\frac{t}{\tau}}}_{\text{Risp. transitoria}} + \underbrace{E}_{\text{Risp. a regime}} \] divisa in:
- risposta transitoria, che influenza la tensione durante il transitorio;
- risposta a regime, che indica la tensione presente una volta esaurito il transitorio.
- evoluzione libera, ovvero ciò che è dovuto al comportamento del condensatore;
- risposta forzata, ovvero ciò che è dovuto a fattori esterni.
Dimostrazione:
Al fine di dimostrare le varie formule consideriamo che la variabile di stato del circuito (data la presenza del condensatore) è la tensione \( v_C(t)\), da cui poi sarà possibile risolvere il circuito nella sua totalità.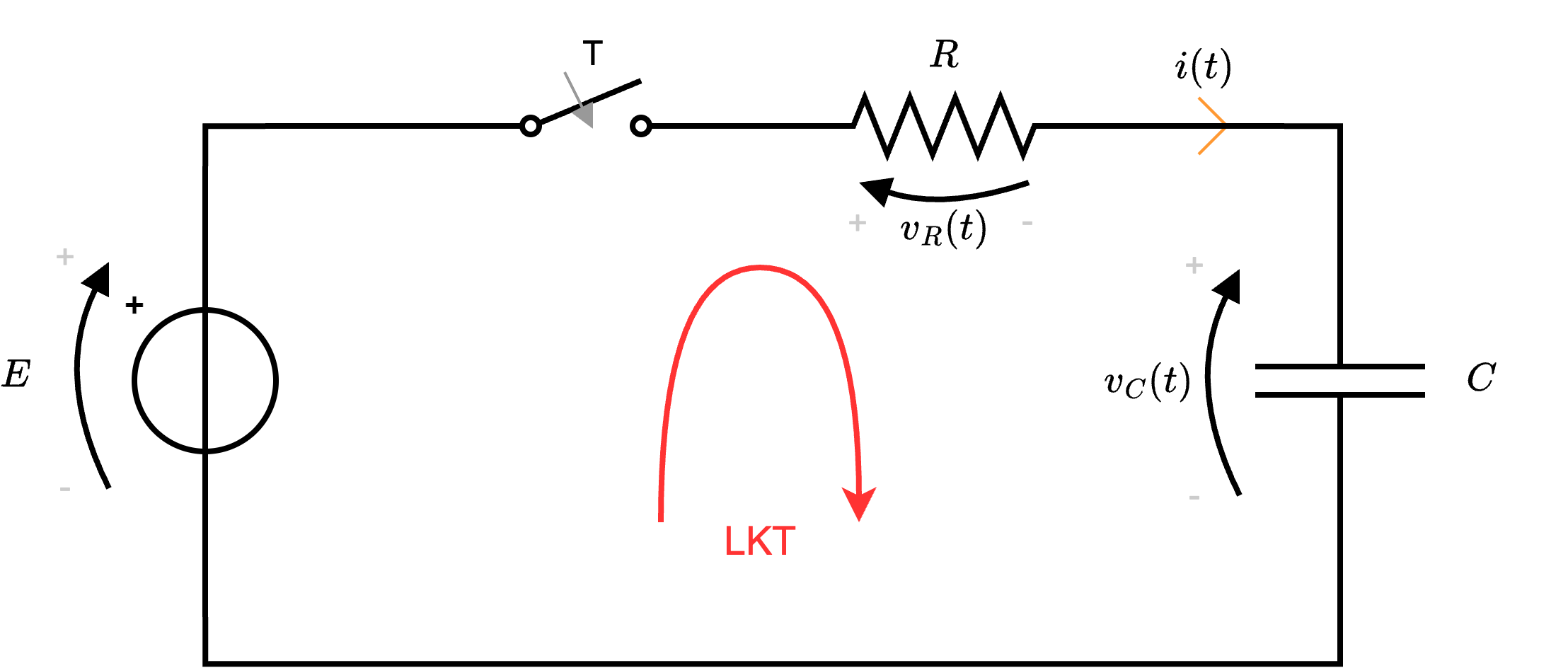 
da cui si ottiene la seguente equazione \[ LKT: \quad E - v_R(t) - v_C(t) = 0 \] Considerando ora le equazioni costitutive dei componenti, ovvero \[ \left\{ \begin{array}{ccl} v_R(t) & = & R \cdot i(t) \\ i(t) & = & C \cdot \frac{d}{d t} v_C(t) \end{array} \right. \quad \implies \quad v_R = R \cdot C \cdot \frac{d}{d t} v_C(t) \] e sostituendo, si ottiene \[ LKT: \quad E - R \cdot C \cdot \frac{d}{d t} v_C(t) - v_C(t) = 0 \] che, riordinata, diventerebbe \[ LKT: \quad \frac{d}{d t} v_C(t) + \frac{1}{R \cdot C} \cdot v_C(t) = \frac{E}{R \cdot C} \] che è una equazione differenziale ordinaria a coefficienti costanti del primo ordine, che è possibile risolvere utilizzando il metodo di Cauchy.
Considerando le ipotesi iniziali, cioè \[ v_C(t_0 = 0^-) = v_{C0} \] e che la tensione è una variabile di stato (che non può variare istantaneamente), vale \[ v_C(0^-) = v_C(0^+) = v_C(0) = v_{C0} \] si ha che è possibile risolvere \[ \left\{ \begin{array}{ccl} \frac{d}{d t} v_C(t) + \frac{1}{R \cdot C} \cdot v_C(t) & = & \frac{E}{R \cdot C} \\ v_C(0) & = & v_{C0} \end{array} \right. \] Seguendo il metodo di Cauchy, si ha che la soluzione di tale equazione differenziale è data dalla somma della soluzione dell'omogenea associata \( o(t)\) e dalla soluzione particolare \( p(t)\), cioè \[ v_C(t) = o(t) + p(t) \]
Al fine di calcolarle, consideriamo che \( B\) è una soluzione (anche se particolare) dell'equazione, per cui si ha che è possibile sostituirla all'equazione iniziale \[ \begin{array}{lccl} LKT \ \text{sol. particolare}: & \overbrace{\frac{d}{d t} B}^0 + \frac{1}{R \cdot C} \cdot B & = & \frac{E}{R \cdot C} \\ & \frac{B}{R \cdot C} & = & \frac{E}{R \cdot C} \\ & B & = & E \end{array} \] Per calcolare \( A\), è invece possibile considerare che conosciamo il valore di \( v_C(0)\) ed è quindi possibile calcolare \[ \begin{array}{ccl} v_{C0} & = & v_C(0) \\ & = & A \cdot \mathrm{e}^{-\frac{0}{R \cdot C}} + E \\ & = & A + E \end{array} \] ovvero è necessario risolvere la seguente equazione in \( A\) \[ v_{C0} = A + E \qquad \implies \qquad A = v_{C0} - E \] per cui, si ha che la soluzione dell'equazione è \[ v_C(t) = (v_{C0} - E) \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} + E \]
Tensione ai capi del condensatore
Al fine di calcolare la tensione \( v_C(t)\), consideriamo di applicare LKTConsiderando le ipotesi iniziali, cioè \[ v_C(t_0 = 0^-) = v_{C0} \] e che la tensione è una variabile di stato (che non può variare istantaneamente), vale \[ v_C(0^-) = v_C(0^+) = v_C(0) = v_{C0} \] si ha che è possibile risolvere \[ \left\{ \begin{array}{ccl} \frac{d}{d t} v_C(t) + \frac{1}{R \cdot C} \cdot v_C(t) & = & \frac{E}{R \cdot C} \\ v_C(0) & = & v_{C0} \end{array} \right. \] Seguendo il metodo di Cauchy, si ha che la soluzione di tale equazione differenziale è data dalla somma della soluzione dell'omogenea associata \( o(t)\) e dalla soluzione particolare \( p(t)\), cioè \[ v_C(t) = o(t) + p(t) \]
Calcolo della soluzione dell'omogenea associata
Al fine di calcolare \( o(t)\), si ha che è necessario risolvere l'equazione differenziale omogenea associata \[ \frac{d}{d t} v_C(t) + \frac{1}{R \cdot C} \cdot v_C(t) = 0 \] e, per farlo, consideriamo il polinomio caratteristico associato (dato dalle incognite dello stesso grado del grado di derivazione) \[ \lambda + \frac{1}{R \cdot C} = 0 \] e la sua soluzione \[ \lambda = -\frac{1}{R \cdot C} \] che ci porta alla soluzione \[ o(t) = A \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} \]Calcolo della soluzione particolare
Al fine di calcolare la soluzione particolare \( p(t)\), si ha che è necessario considerare il termine noto dell'equazione \( b(t)\), uguale a \[ b(t) = \frac{E}{R \cdot C} \] che è una costante: si ha quindi che anche la soluzione particolare avrà la forma della costante, ovvero \[ b(t) = B \]Calcolo dei coefficienti
Fino ad ora, si è ottenuta la seguente soluzione \[ v_C(t) = A \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} + B \] con incognite le costanti \( A\) e \( B\).Al fine di calcolarle, consideriamo che \( B\) è una soluzione (anche se particolare) dell'equazione, per cui si ha che è possibile sostituirla all'equazione iniziale \[ \begin{array}{lccl} LKT \ \text{sol. particolare}: & \overbrace{\frac{d}{d t} B}^0 + \frac{1}{R \cdot C} \cdot B & = & \frac{E}{R \cdot C} \\ & \frac{B}{R \cdot C} & = & \frac{E}{R \cdot C} \\ & B & = & E \end{array} \] Per calcolare \( A\), è invece possibile considerare che conosciamo il valore di \( v_C(0)\) ed è quindi possibile calcolare \[ \begin{array}{ccl} v_{C0} & = & v_C(0) \\ & = & A \cdot \mathrm{e}^{-\frac{0}{R \cdot C}} + E \\ & = & A + E \end{array} \] ovvero è necessario risolvere la seguente equazione in \( A\) \[ v_{C0} = A + E \qquad \implies \qquad A = v_{C0} - E \] per cui, si ha che la soluzione dell'equazione è \[ v_C(t) = (v_{C0} - E) \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} + E \]
Corrente del circuito
Una volta calcolata la tensione, è possibile calcolare anche la corrente del circuito. Considerando che sono componenti in serie, si ha che è possibile calcolarla considerando l'equazione costitutiva del condensatore, ovvero \[ \begin{array}{ccl} i_C(t) & = & C \cdot \frac{d}{d t} v_C(t) \\ & = & C \cdot \frac{d}{d t} \left[ (v_{C0} - E) \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} + E \right] \\ & = & C \cdot (v_{C0} - E) \cdot \left( -\frac{1}{R \cdot C} \right) \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} \\ & = & (v_{C0} - E) \cdot \left( -\frac{1}{R} \right) \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} \\ & = & \frac{E - v_{C0}}{R} \cdot \mathrm{e}^{-\frac{t}{R \cdot C}} \end{array} \] Si è quindi dimostrata la proposizione.Dimostrazione - Circuiti RL
Data la proposizione
Enunciato:
Considerando un circuito RL (formato da una resistenza \( R\) e un induttore \( L\)) 
sotto le seguenti ipotesi:
Si definisce infatti la corrente \[ i(t) = \underbrace{\left( I_{L0} - \frac{E}{R} \right) \cdot \mathrm{e}^{-\frac{t}{\tau}}}_{\text{Risp. transitoria}} + \underbrace{\frac{E}{R}}_{\text{Risp. a regime}} \] divisa in: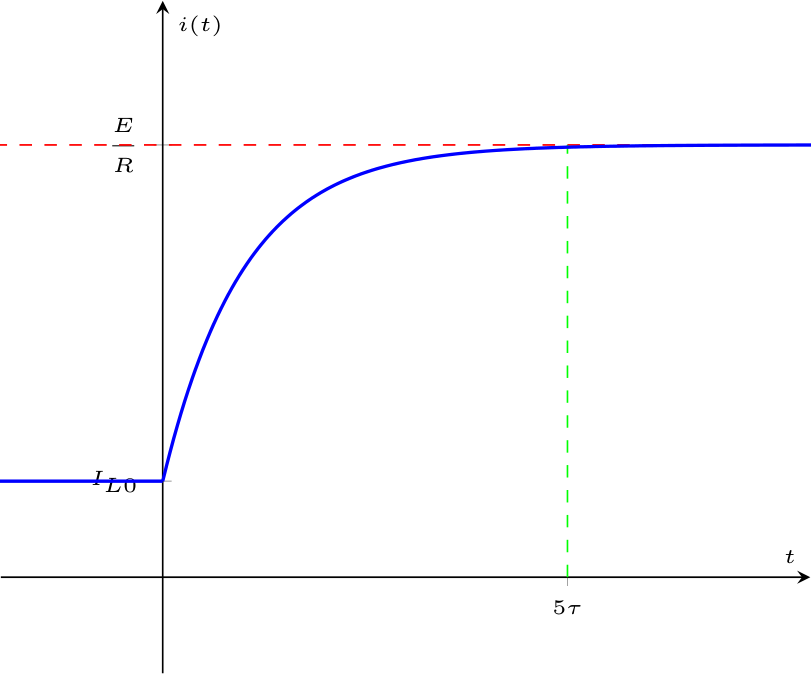
In maniera analoga, è possibile vedere la funzione \[ i(t) = \underbrace{I_{L0} \cdot \mathrm{e}^{-\frac{t}{\tau}}}_{\text{evoluzione libera}} + \underbrace{E \cdot \left( 1 - \mathrm{e}^{-\frac{t}{\tau}} \right)}_{\text{risposta forzata}} \] divisa in: 
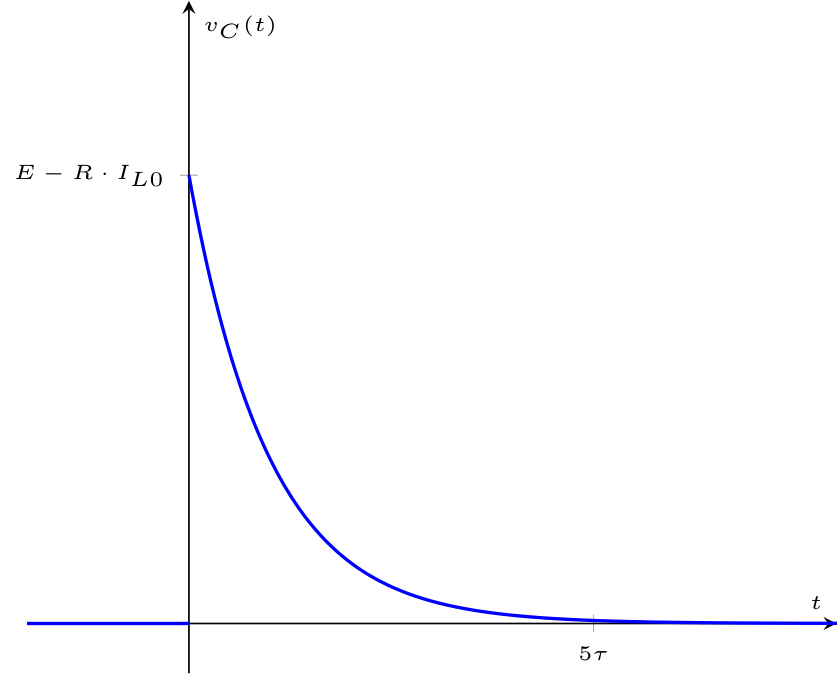Come è evidente dal grafico, la tensione varia istantaneamente partendo dal valore nullo per poi raggiungere il massimo istantaneamente ed infine decrescere.
- l' induttore inizialmente ha una certa energia \( I_{L0}\), ovvero la corrente iniziale (all'istante \( t_0 = 0^-\)) dell'induttore è uguale a \( I_{L0}\), cioè \[ i(t_0 = 0^-) = I_{L0} \]
- all'istante \( t_1 = 0 \mathrm{ \, s }\), il derivatore D si sposta in posizione 1..
Corrente del circuito
La corrente dell'induttore (e quindi, dato che i componenti sono in serie, del circuito) \( i(t)\) ha il seguente comportamento \[ i(t) = \left( I_{L0} - \frac{E}{R} \right) \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} + \frac{E}{R} \]Costante di tempo del sistema
È possibile definire la costante di tempo del sistema \( \tau\) (misurata in secondi \( \mathrm{ \, s }\)) che informa del tempo di risposta del circuito: \[ \tau = \frac{L}{R} \] ed è quindi possibile riscrivere la funzione \( i(t)\) come \[ i(t) = \left( I_{L0} - \frac{E}{R} \right) \cdot \mathrm{e}^{-\frac{t}{\tau}} + \frac{E}{R} \]Tensioni ai capi dell'induttore
La tensione \( v_L(t)\) ha il seguente comportamento \[ v_L(t) = \left( E - R \cdot I_{L0} \right) \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} \]Interpretazione delle funzioni
È possibile interpretare la funzione \( i(t)\) al fine di capire l'evoluzione dell'energia dell'induttore.Si definisce infatti la corrente \[ i(t) = \underbrace{\left( I_{L0} - \frac{E}{R} \right) \cdot \mathrm{e}^{-\frac{t}{\tau}}}_{\text{Risp. transitoria}} + \underbrace{\frac{E}{R}}_{\text{Risp. a regime}} \] divisa in:
- risposta transitoria, che influenza la corrente durante il transitorio;
- risposta a regime, che indica la corrente presente una volta esaurito il transitorio.
- evoluzione libera, ovvero ciò che è dovuto al comportamento dell'induttore;
- risposta forzata, ovvero ciò che è dovuto a fattori esterni.
Dimostrazione:
Al fine di dimostrare le varie formule consideriamo che la variabile di stato del circuito (data la presenza dell'induttore) è la corrente \( i(t)\), da cui poi sarà possibile risolvere il circuito nella sua totalità.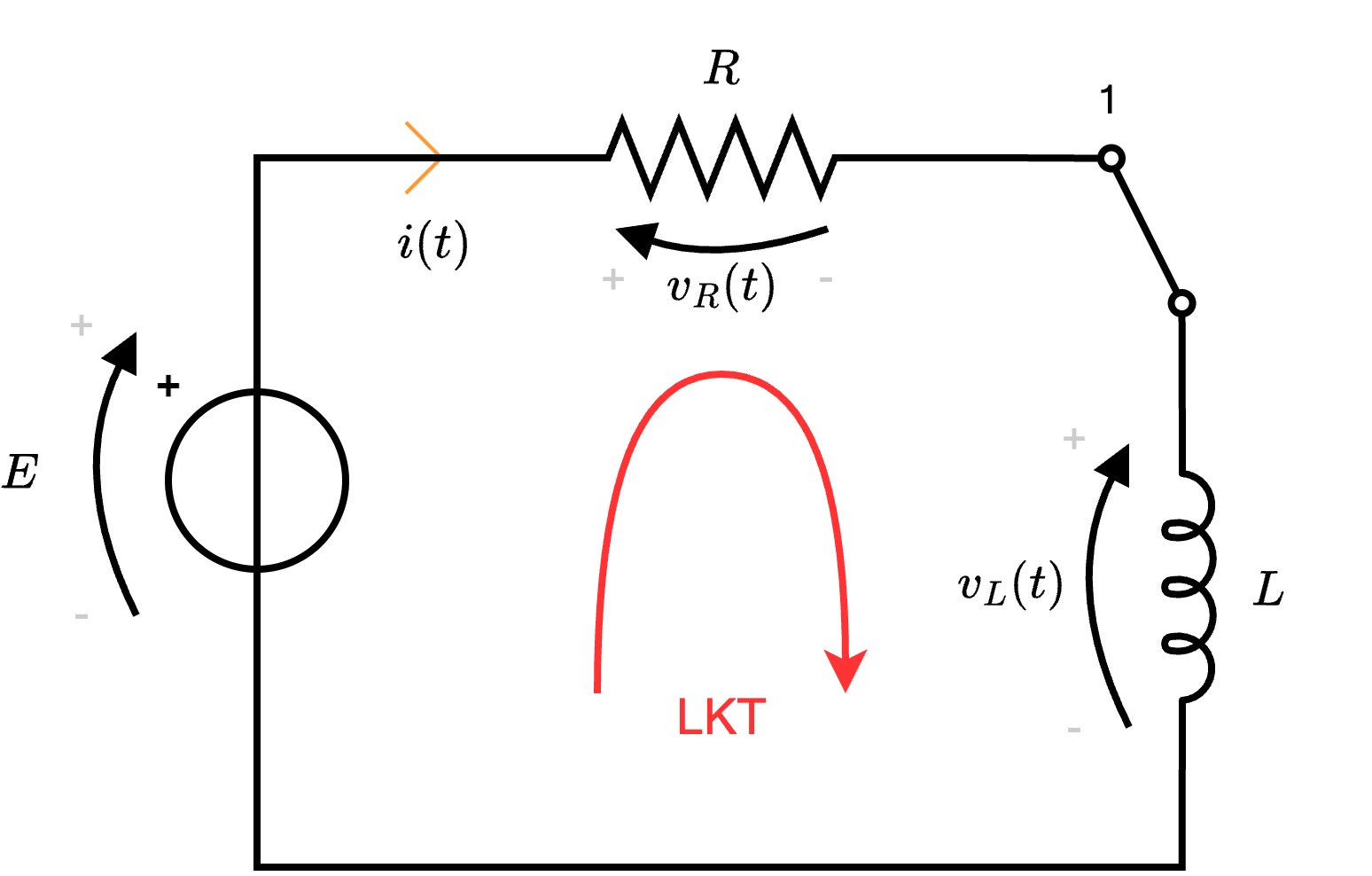 
Considerando ora le equazioni costitutive dei componenti, ovvero \[ \left\{ \begin{array}{ccl} v_R(t) & = & R \cdot i(t) \\ v_L(t) & = & L \cdot \frac{d}{d t} i(t) \end{array} \right. \] e, sostituendo, si ottiene \[ LKT: \quad E - R \cdot i(t) - L \cdot \frac{d}{d t} i(t) = 0 \] che, riordinata, diventerebbe \[ LKT: \quad \frac{d}{d t} i(t) + \frac{R}{L} \cdot i(t) = \frac{E}{L} \] che è una equazione differenziale ordinaria a coefficienti costanti del primo ordine, che è possibile risolvere utilizzando il metodo di Cauchy.
Considerando le ipotesi iniziali, cioè \[ i(t_0 = 0^-) = I_{L0} \] e che la corrente è una variabile di stato (che non può variare istantaneamente), vale \[ i(0^-) = i(0^+) = i(0) = I_{L0} \] si ha che è possibile risolvere \[ \left\{ \begin{array}{ccl} \frac{d}{d t} i(t) + \frac{R}{L} \cdot i(t) = \frac{E}{L} \\ i(0) & = & I_{L0} \end{array} \right. \] Seguendo il metodo di Cauchy, si ha che la soluzione di tale equazione differenziale è data dalla somma della soluzione dell'omogenea associata \( o(t)\) e dalla soluzione particolare \( p(t)\), cioè \[ i(t) = o(t) + p(t) \]
Al fine di calcolarle, consideriamo che \( B\) è una soluzione (anche se particolare) dell'equazione, per cui si ha che è possibile sostituirla all'equazione iniziale \[ \begin{array}{lccl} LKT \ \text{sol. particolare}: & \overbrace{\frac{d}{d t} B}^0 + \frac{R}{L} \cdot B & = & \frac{E}{L} \\ LKT \ \text{sol. particolare}: & \frac{R}{L} \cdot B & = & \frac{E}{L} \\ LKT \ \text{sol. particolare}: & R \cdot B & = & E \\ LKT \ \text{sol. particolare}: & B & = & \frac{E}{R} \end{array} \] Per calcolare \( A\), è invece possibile considerare che conosciamo il valore di \( i(0)\), ed è quindi possibile calcolare \[ \begin{array}{ccl} I_{L0} & = & i(0) \\ & = & A \cdot \mathrm{e}^{-\frac{R}{L} \cdot 0} + \frac{E}{R} \\ & = & A + \frac{E}{R} \end{array} \] ovvero è necessario risolvere la seguente equazione in \( A\) \[ I_{L0} = A + \frac{E}{R} \qquad \implies \qquad A = I_{L0} - \frac{E}{R} \] per cui, si ha che la soluzione dell'equazione è \[ i(t) = \left( I_{L0} - \frac{E}{R} \right) \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} + \frac{E}{R} \]
Corrente del circuito
Al fine di calcolare la corrente \( i(t)\), consideriamo di applicare LKTConsiderando le ipotesi iniziali, cioè \[ i(t_0 = 0^-) = I_{L0} \] e che la corrente è una variabile di stato (che non può variare istantaneamente), vale \[ i(0^-) = i(0^+) = i(0) = I_{L0} \] si ha che è possibile risolvere \[ \left\{ \begin{array}{ccl} \frac{d}{d t} i(t) + \frac{R}{L} \cdot i(t) = \frac{E}{L} \\ i(0) & = & I_{L0} \end{array} \right. \] Seguendo il metodo di Cauchy, si ha che la soluzione di tale equazione differenziale è data dalla somma della soluzione dell'omogenea associata \( o(t)\) e dalla soluzione particolare \( p(t)\), cioè \[ i(t) = o(t) + p(t) \]
Calcolo della soluzione dell'omogenea associata
Al fine di calcolare \( o(t)\), si ha che è necessario risolvere l'equazione differenziale omogenea associata \[ \frac{d}{d t} i(t) + \frac{R}{L} \cdot i(t) = 0 \] e, per farlo, consideriamo il polinomio caratteristico associato (dato dalle incognite dello stesso grado del grado di derivazione) \[ \lambda + \frac{R}{L} = 0 \] e la sua soluzione \[ \lambda = -\frac{R}{L} \] che ci porta alla soluzione \[ o(t) = A \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} \]Calcolo della soluzione particolare
Al fine di calcolare la soluzione particolare \( p(t)\), si ha che è necessario considerare il termine noto dell'equazione \( b(t)\), uguale a \[ b(t) = \frac{E}{L} \] che è una costante: si ha quindi che anche la soluzione particolare avrà la forma della costante, ovvero \[ b(t) = B \]Calcolo dei coefficienti
Fino ad ora, si è ottenuta la seguente soluzione \[ i(t) = A \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} + B \] con incognite le costanti \( A\) e \( B\).Al fine di calcolarle, consideriamo che \( B\) è una soluzione (anche se particolare) dell'equazione, per cui si ha che è possibile sostituirla all'equazione iniziale \[ \begin{array}{lccl} LKT \ \text{sol. particolare}: & \overbrace{\frac{d}{d t} B}^0 + \frac{R}{L} \cdot B & = & \frac{E}{L} \\ LKT \ \text{sol. particolare}: & \frac{R}{L} \cdot B & = & \frac{E}{L} \\ LKT \ \text{sol. particolare}: & R \cdot B & = & E \\ LKT \ \text{sol. particolare}: & B & = & \frac{E}{R} \end{array} \] Per calcolare \( A\), è invece possibile considerare che conosciamo il valore di \( i(0)\), ed è quindi possibile calcolare \[ \begin{array}{ccl} I_{L0} & = & i(0) \\ & = & A \cdot \mathrm{e}^{-\frac{R}{L} \cdot 0} + \frac{E}{R} \\ & = & A + \frac{E}{R} \end{array} \] ovvero è necessario risolvere la seguente equazione in \( A\) \[ I_{L0} = A + \frac{E}{R} \qquad \implies \qquad A = I_{L0} - \frac{E}{R} \] per cui, si ha che la soluzione dell'equazione è \[ i(t) = \left( I_{L0} - \frac{E}{R} \right) \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} + \frac{E}{R} \]
Tensione ai capi dell'induttore
Una volta calcolata la corrente, è possibile calcolare anche la tensione ai capi dell'induttore. Considerando l'equazione costitutiva, ovvero \[ \begin{array}{ccl} v_L(t) & = & L \cdot \frac{d}{d t} i(t) \\ & = & L \cdot \frac{d}{d t} \left[ \left( I_{L0} - \frac{E}{R} \right) \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} + \frac{E}{R} \right] \\ & = & L \cdot \left( I_{L0} - \frac{E}{R} \right) \cdot \left( -\frac{R}{L} \right) \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} \\ & = & \left( I_{L0} - \frac{E}{R} \right) \cdot ( -R ) \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} \\ & = & \left( E - R \cdot I_{L0} \right) \cdot \mathrm{e}^{-\frac{R}{L} \cdot t} \end{array} \] Si è quindi dimostrata la proposizione.Dimostrazione - Struttura generica di variabili di stato
Data la proposizione
Enunciato:
Considerando un circuito RC o RL, è possibile calcolare la variabile di stato come \[ x(t) = (x_0 - x_\infty) \cdot \mathrm{e}^{-\frac{t}{\tau}} + x_\infty \] dove:
- \( x_0\) è la condizione iniziale della variabile;
- \( x_\infty\) è la risposta a regime (ovvero il valore assunto quando il circuito è a regime);
- \( \tau\) è la costante di tempo del sistema (uguale a \( R \cdot C\) per circuiti RC ed \( \frac{L}{R}\) per circuiti RL, dove \( R\) è la resistenza equivalente del circuito vista dal componente).
Dimostrazione:
Considerando le equazioni differenziali relative ai circuiti RC \[ \frac{d}{d t} v_C(t) + \frac{1}{R \cdot C} \cdot v_C(t) = \frac{E}{R \cdot C} \] e ai circuiti RL \[ \frac{d}{d t} i(t) + \frac{R}{L} \cdot i(t) = \frac{E}{L} \] è possibile sostituire con \( \tau\) le relative costanti di tempo e ricondursi all'equazione differenziale \[ \frac{d}{d t} x(t) + \frac{i(t)}{\tau} = x_F \] dove \( x_F\) è detto valore "forzante", dovuto al generatore.
Consideriamo inoltre il valore di energia iniziale come \( x_0\).
Si ha quindi che è necessario risolvere la seguente equazione differenziale \[ \left\{ \begin{array}{l} \frac{d}{d t} x(t) + \frac{i(t)}{\tau} = x_F \\ x(t = 0^-) = x(t = 0) = x_0 \end{array} \right. \] Si sa inoltre che le equazioni differenziali di questo tipo hanno soluzioni del tipo \[ \begin{array}{ccl} x(t) & = & o(t) + p(t) \\ & = & x_T(t) + x_\infty \end{array} \] In particolare, la soluzione \( o(t)\) è uguale a \[ o(t) = A \cdot \mathrm{e}^{-\frac{t}{\tau}} \] e che, al fine di calcolare il valore del coefficiente \( A\), è sufficiente considerare le condizioni iniziali, ovvero \[ \begin{array}{ccl} x_0 & = & x(0) \\ & = & A \cdot \mathrm{e}^{-\frac{0}{\tau}} + x_\infty \\ & = & A + x_\infty \end{array} \] ovvero è sufficiente risolvere l'equazione \[ x_0 = A + x_\infty \qquad \implies \qquad A = x_0 - x_\infty \] e, quindi, è possibile dire che \( x(t)\) è uguale a \[ x(t) = (x_0 - x_\infty) \cdot \mathrm{e}^{-\frac{t}{\tau}} + x_\infty \]
Consideriamo inoltre il valore di energia iniziale come \( x_0\).
Si ha quindi che è necessario risolvere la seguente equazione differenziale \[ \left\{ \begin{array}{l} \frac{d}{d t} x(t) + \frac{i(t)}{\tau} = x_F \\ x(t = 0^-) = x(t = 0) = x_0 \end{array} \right. \] Si sa inoltre che le equazioni differenziali di questo tipo hanno soluzioni del tipo \[ \begin{array}{ccl} x(t) & = & o(t) + p(t) \\ & = & x_T(t) + x_\infty \end{array} \] In particolare, la soluzione \( o(t)\) è uguale a \[ o(t) = A \cdot \mathrm{e}^{-\frac{t}{\tau}} \] e che, al fine di calcolare il valore del coefficiente \( A\), è sufficiente considerare le condizioni iniziali, ovvero \[ \begin{array}{ccl} x_0 & = & x(0) \\ & = & A \cdot \mathrm{e}^{-\frac{0}{\tau}} + x_\infty \\ & = & A + x_\infty \end{array} \] ovvero è sufficiente risolvere l'equazione \[ x_0 = A + x_\infty \qquad \implies \qquad A = x_0 - x_\infty \] e, quindi, è possibile dire che \( x(t)\) è uguale a \[ x(t) = (x_0 - x_\infty) \cdot \mathrm{e}^{-\frac{t}{\tau}} + x_\infty \]
Nota bene - Vero per ogni variabile di rete
Tale struttura è valida per qualsiasi variabile di rete. Sarà tuttavia utilizzabile solamente per le variabili di stato del sistema, dato che sono le uniche il cui valore non può variare istantaneamente (e quindi \( x(0^-) = x(0^+) = x_0\)).
Definizione - Comportamento a regime di condensatori e induttori
Considerando circuiti composti da componenti dinamici, si ha che essi contribuiscono a causare transitori.
Quando ciò non avviene, ovvero il circuito è a regime, questi componenti "modificano" la topologia del circuito. Si ha infatti che la variabile di stato non subisce variazioni durante il tempo, ovvero (considerando \( x(t)\) la variabile di stato) \[ \frac{d}{d t} x(t) = 0 \]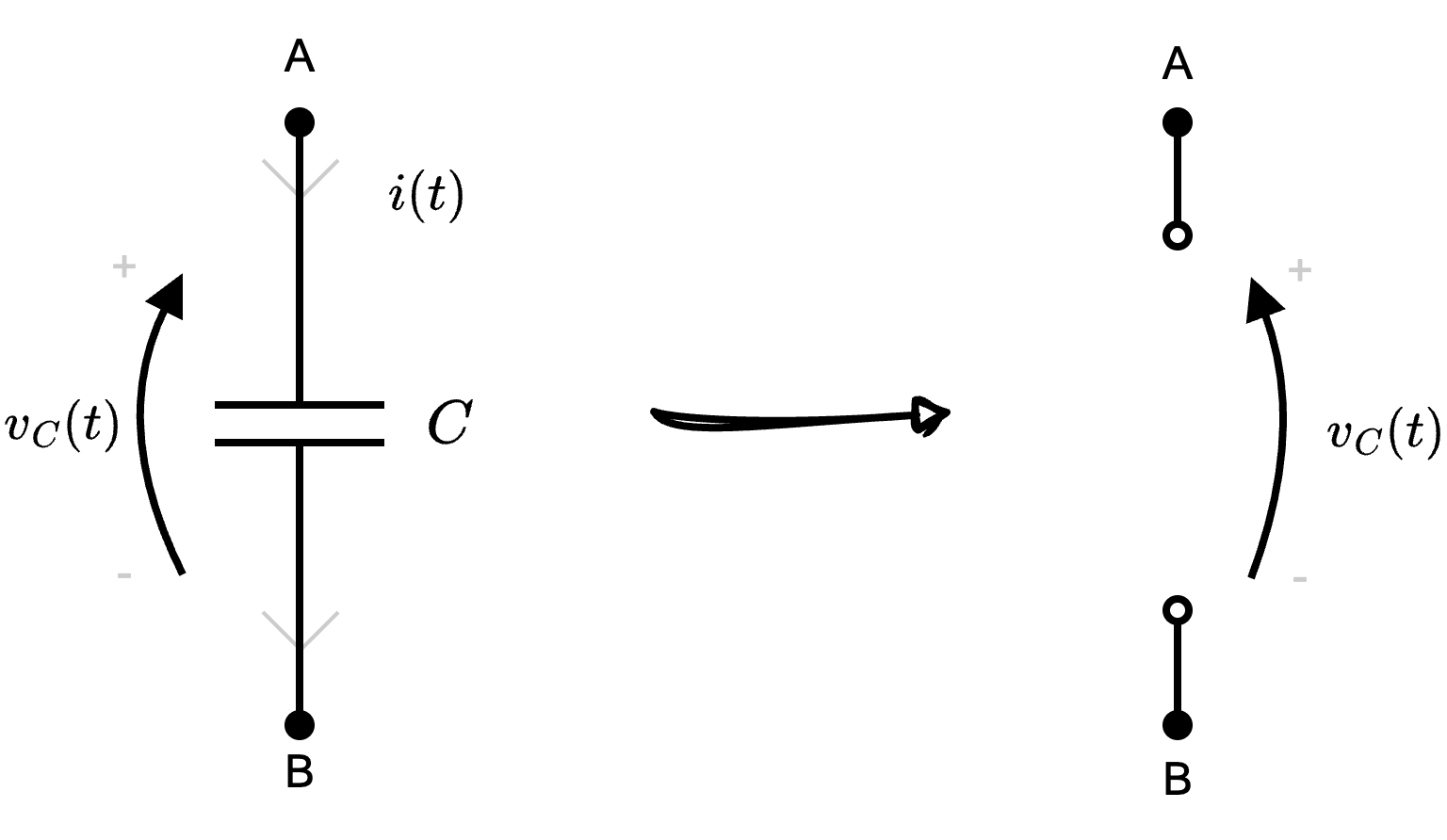
Quando ciò non avviene, ovvero il circuito è a regime, questi componenti "modificano" la topologia del circuito. Si ha infatti che la variabile di stato non subisce variazioni durante il tempo, ovvero (considerando \( x(t)\) la variabile di stato) \[ \frac{d}{d t} x(t) = 0 \]
Comportamento a regime di condensatori
Considerando un condensatore, la cui equazione costitutiva è \[ i(t) = C \cdot \frac{d}{d t} v_C(t) \] si ha che a regime non vi è variazione di tensione \[ \frac{d}{d t} v_C(t) = 0 \] per cui la corrente è nulla \[ i(t) = C \cdot \overbrace{\frac{d}{d t} v_C(t)}^0 \qquad \implies \qquad i(t) = 0 \] e quindi il comportamento è equivalente ad un circuito apertoComportamento a regime di induttori
Considerando un induttore, la cui equazione costitutiva è \[ v_L(t) = L \cdot \frac{d}{d t} i(t) \] si ha che a regime non vi è variazione di corrente \[ \frac{d}{d t} i(t) = 0 \] per cui la tensione è nulla \[ v_L(t) = L \cdot \overbrace{\frac{d}{d t} i(t)}^0 \qquad \implies \qquad v_L(t) = 0 \] e quindi il comportamento è equivalente ad un cortocircuitoEsempio - Risoluzione di un circuito in regime transitorio
Considerando il seguente seguente circuito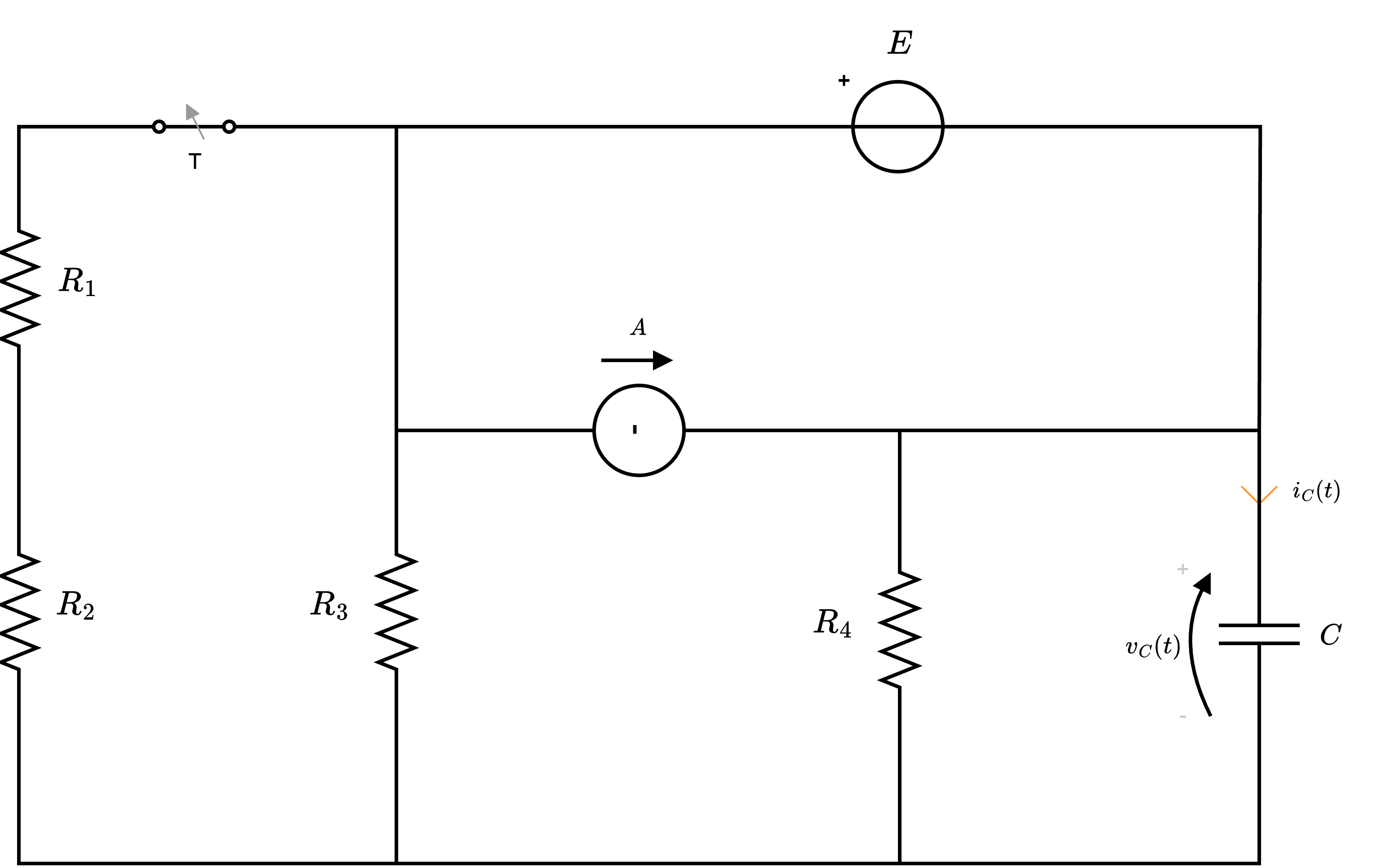 
in cui l'interruttore \( T\) si apre all'istante \( t = 0\mathrm{ \, s }\), calcolare \( v_C(t)\) e \( i_C(t)\).
Calcolare \( v_C(t)\)
Al fine di risolvere questo esercizio, consideriamo che è un circuito RC del primo ordine: ciò comporta che la variabile di stato del circuito è la tensione \( v_C(t)\), in quanto l'equazione costitutiva del condensatore è \[ i_C(t) = C \cdot \frac{d}{dt}v_C(t) \] Data quindi la struttura generica di una variabile di rete, ovvero \[ x(t) = (x_0 - x_\infty) \cdot \mathrm{e}^{-\frac{t}{\tau}} + x_\infty \] applicata alla tensione \( v_C(t)\) si ottiene \[ v_C(t) = (v_C(0) - v_C(\infty)) \cdot \mathrm{e}^{-\frac{t}{R_{eq} \cdot C}} + v_C(\infty) \] in cui è possibile considerare che- la tensione \( v_C(0)\) indica il valore della tensione all'istante \( t = 0\mathrm{ \, s }\). Dato che è una variabile di stato si ha che non può variare istantaneamente e quindi \[ v_C(0) = v_C(0^+) = v_C(0^-) \] È quindi possibile calcolare la tensione all'istante \( t = 0^-\) in cui il circuito è a regime in una situazione in cui l'interrutore \( T\) è ancora chiuso. Si avrà quindi il seguente circuito dove è possibile notare che il condensatore (a regime) si comporta come un circuito aperto.
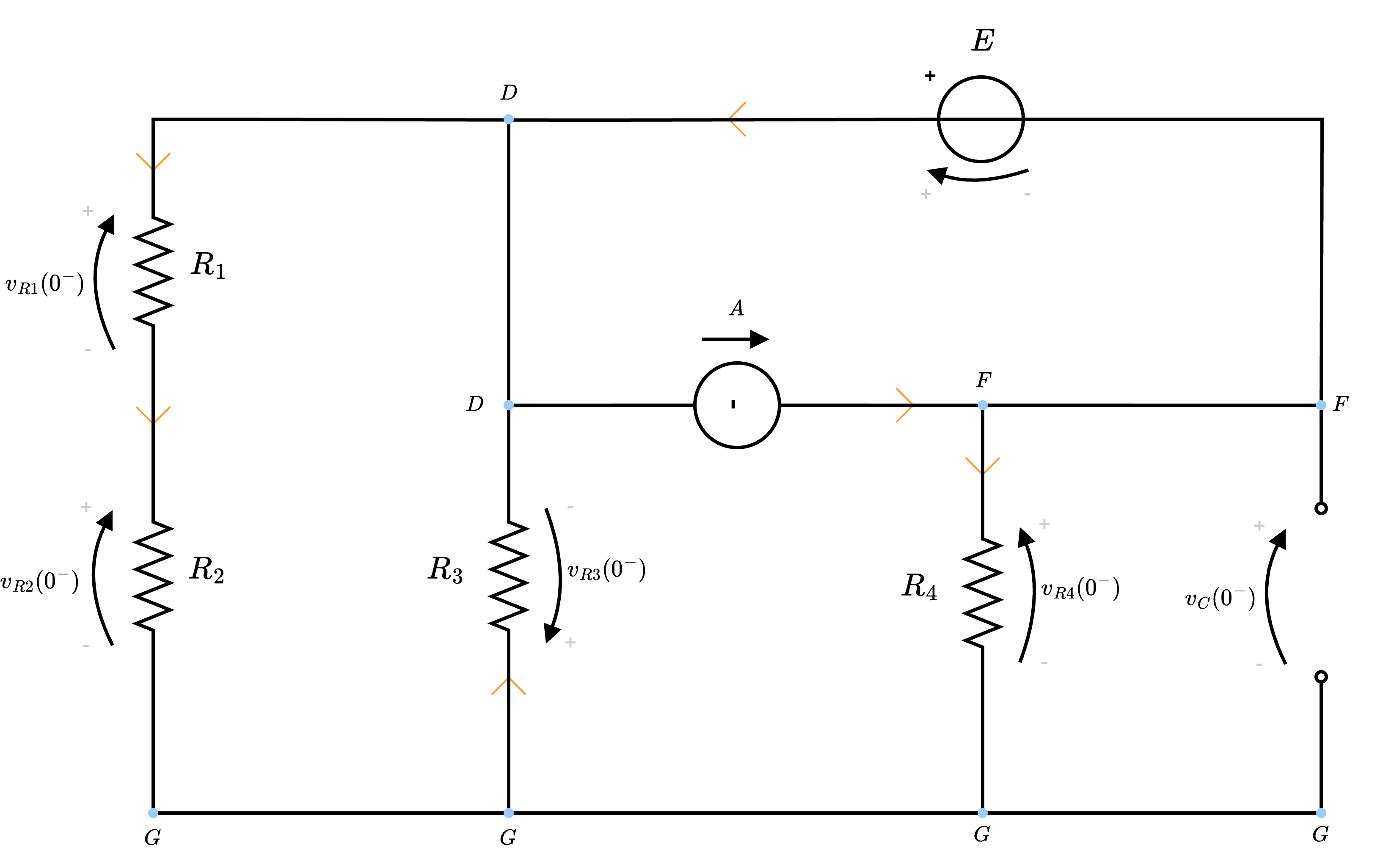
Da ciò, è possibile quindi considerare il seguente circuitoin cui è possibile notare che la tensione \( v_C(t)\) è uguale alla tensione \( v_{R4}(t)\).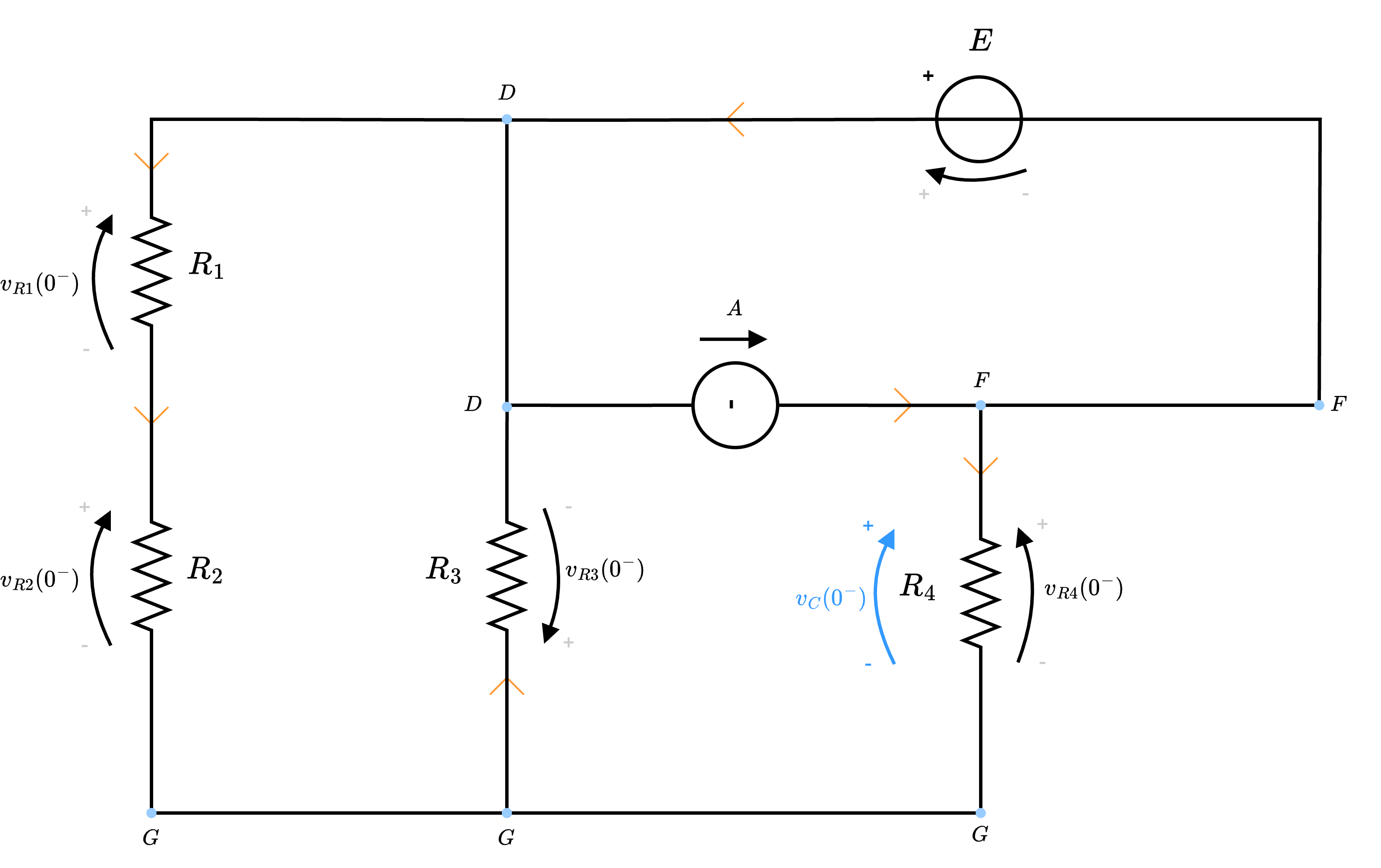
Considerando ora che è possibile riscrivere il circuito nel seguente modosi ha che sono tre lati posti in parallelo (dato che sono collegati ai nodi DF). È quindi possibile dire che tutti i lati hanno la stessa tensione ed è possibile applicare il partitore di tensione per calcolare la tensione \( v_4(t)\), uguale quindi a \[ v_C(0^-) = v_{R4}(0^-) = \frac{R_4}{R_X + R_4} \cdot (-E) \] (ndr, da notare che la tensione \( E\) ha segno negativo perchè il generatore è discorde alle resistenze).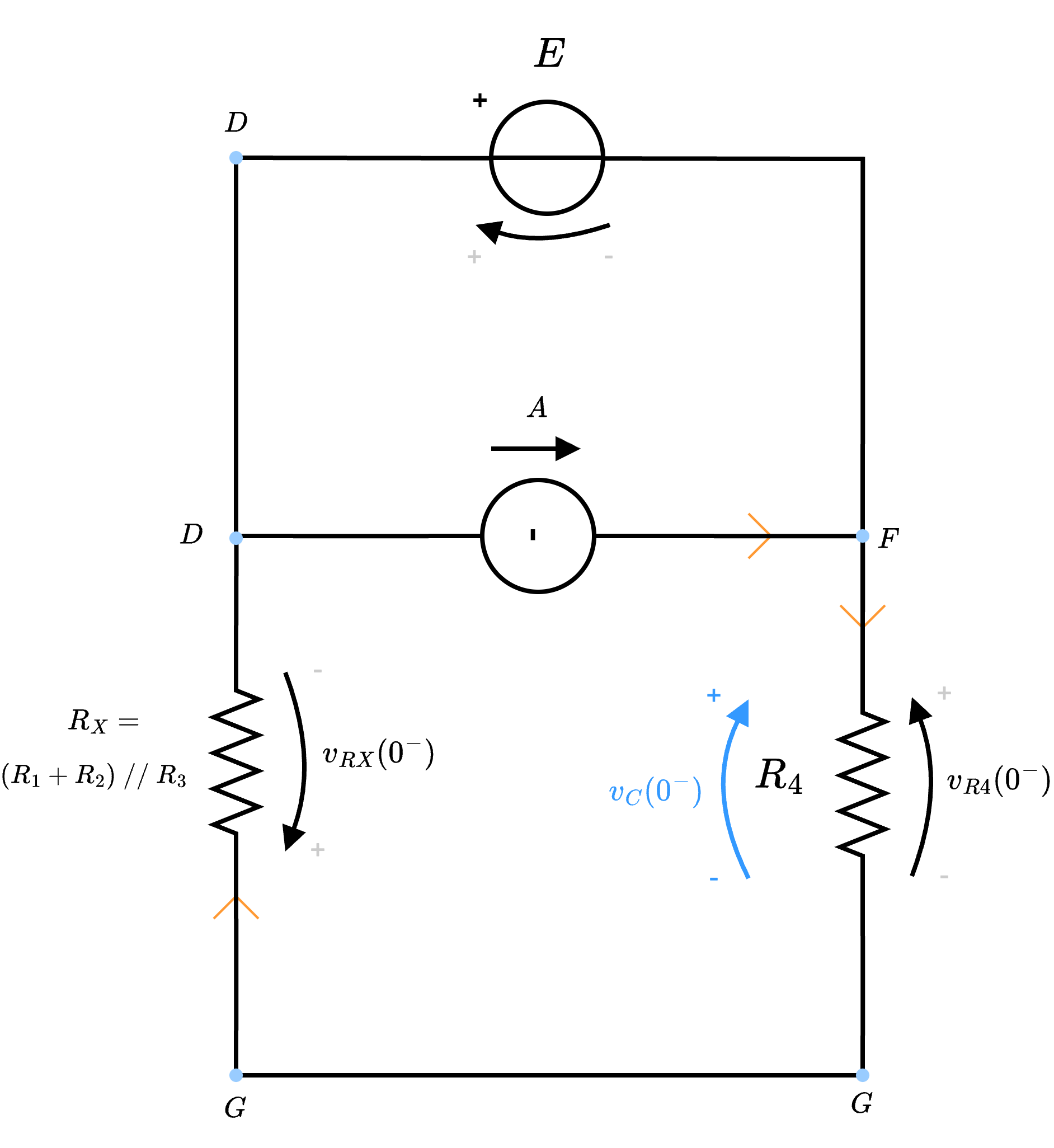
- la tensione \( v_C(\infty)\) indica il valore della tensione a regime, con interruttore \( T\) aperto. Si avrà quindi il seguente circuito (ricordando sempre che il condensatore a regime si comporta come un circuito aperto) che semplificato diventa
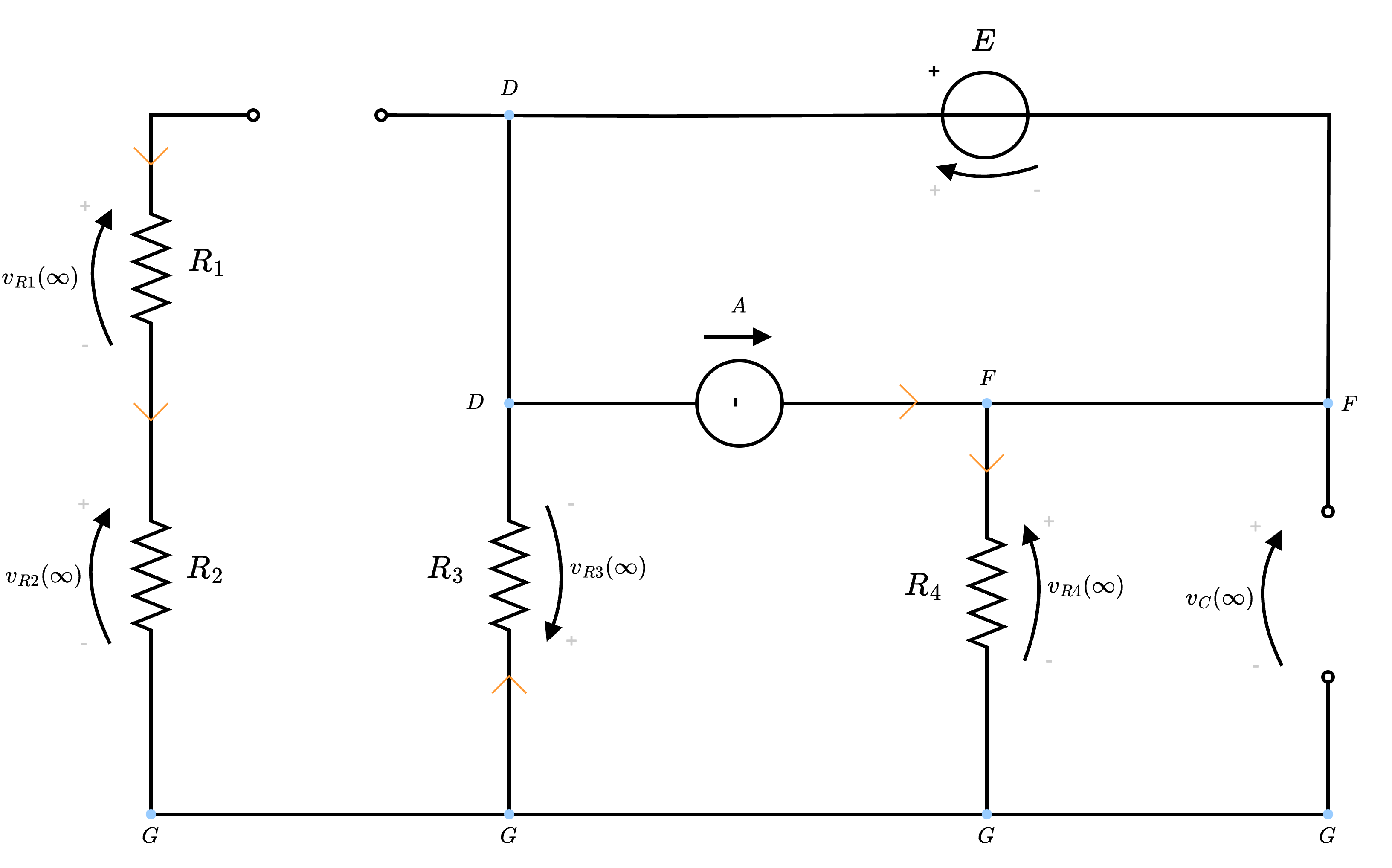che può essere rappresentato nel seguente modo
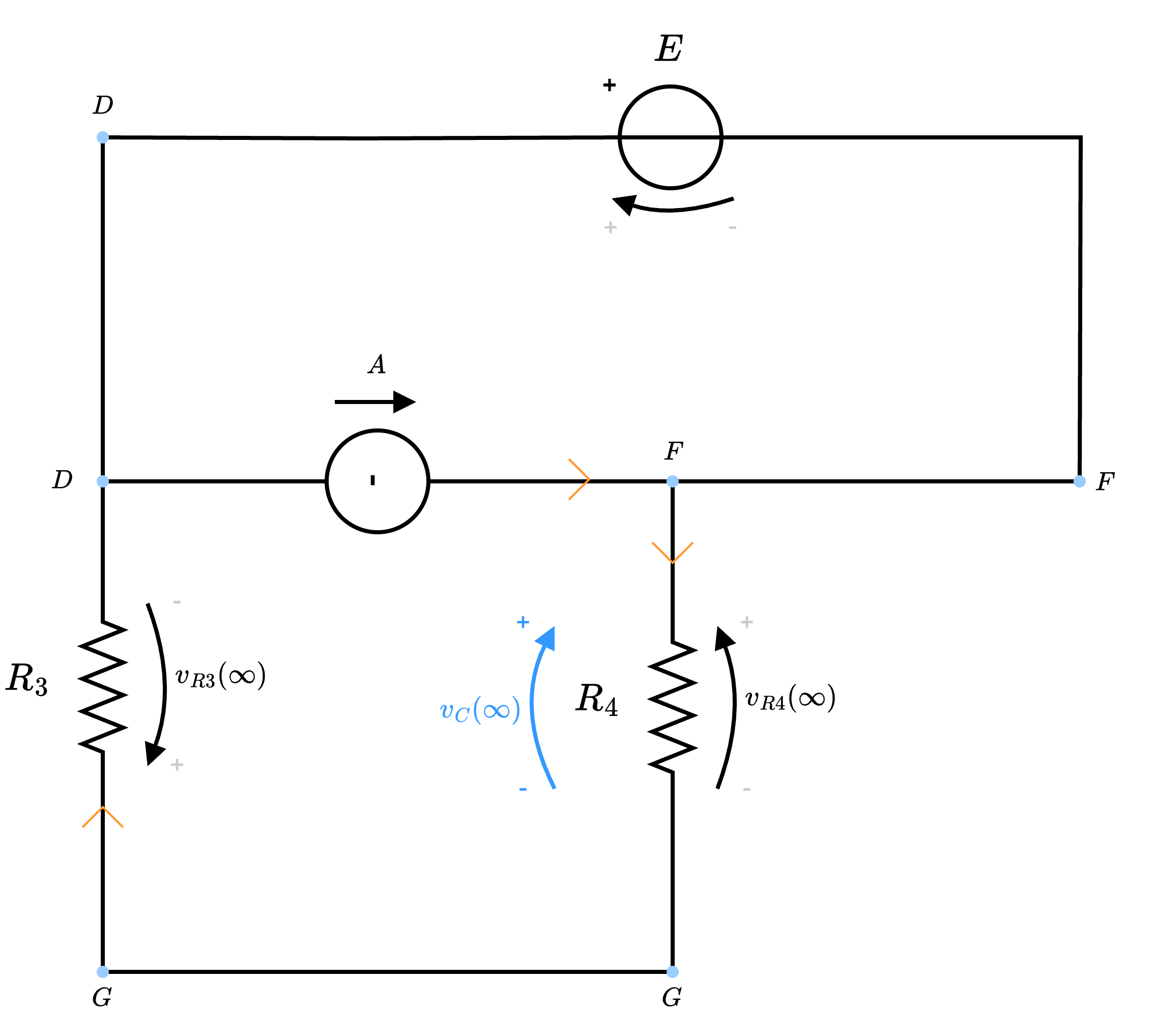Riproponendo il ragionamento fatto per \( v_C(0^-)\), è possibile ottenere che \[ v_C(\infty) = v_{R4}(\infty) = \frac{R_4}{R_3 + R_4} \cdot (-E) \]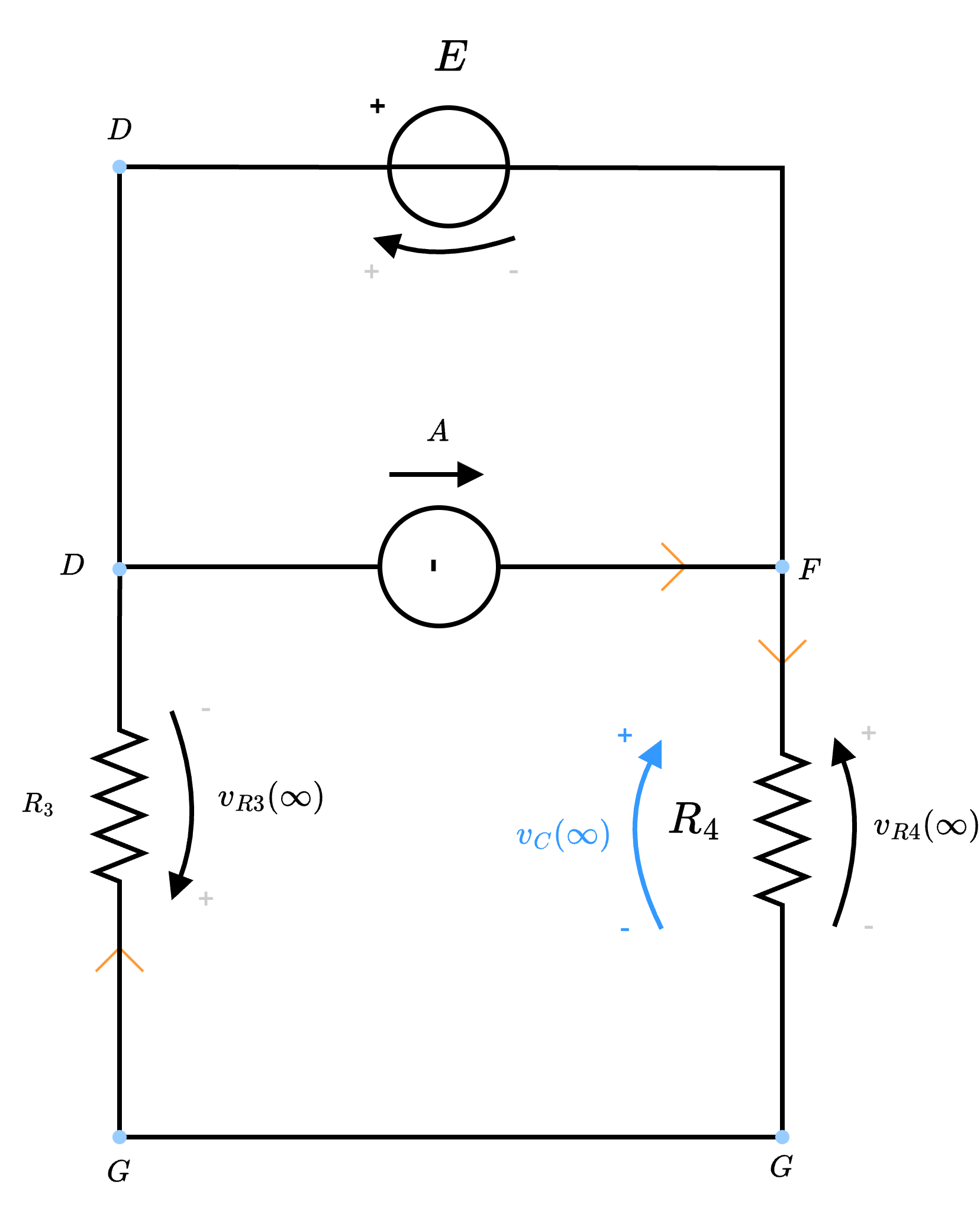
- \( R_{eq}\) è la resistenza equivalente a \( \infty\) "vista" dal condensatore \( C\) e passivando tutti i generatori, calcolabile considerando il seguente circuito che semplificato equivale a
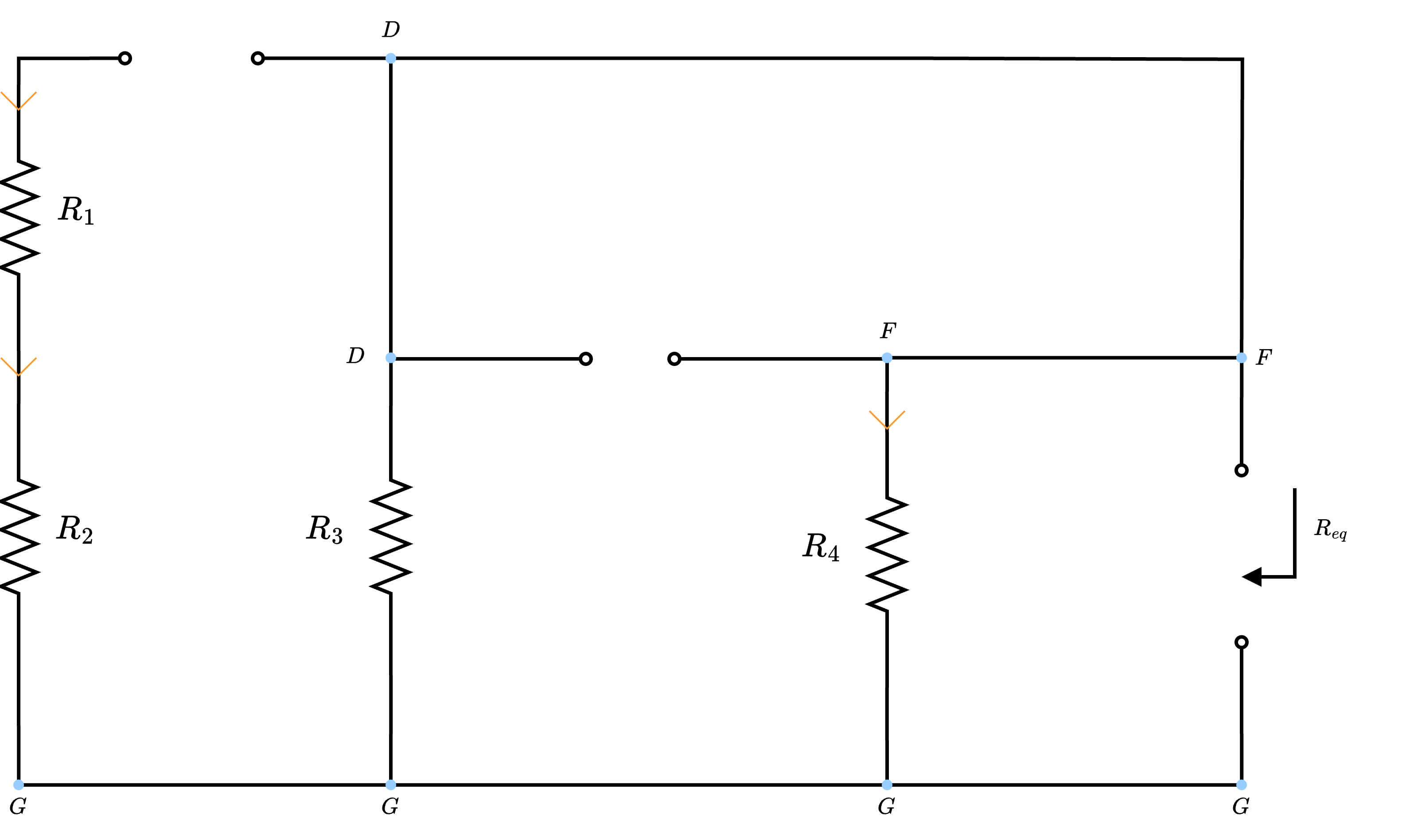ovvero si ha che \[ R_{eq} = R_3 \ // \ R_4 \]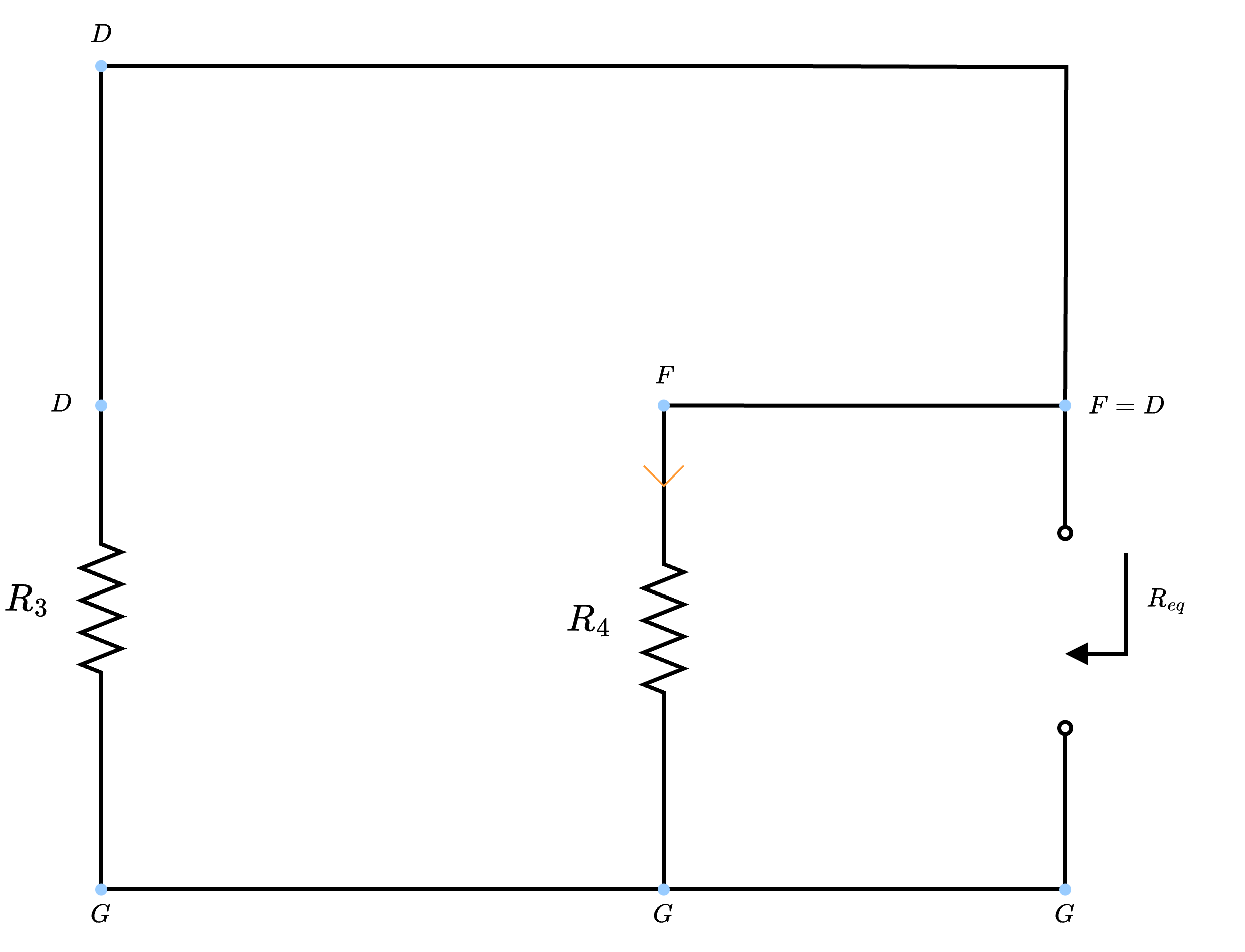
Calcolare \( i_C(t)\)
Una volta calcolato \( v_C(t)\), è possibile calcolare la funzione \( i_C(t)\) considerando l'equazione costitutiva del condensatore, ovvero \[ i_C(t) = C \cdot \frac{d}{dt}v_C(t) \]Definizione - Circuiti RLC (in serie)
Dato un circuito RLC (formato cioè da una resistenza \( R\), un induttore \( L\) e un condensatore \( C\)), esso si presenta nel seguente modo 
è sotto le seguenti ipotesi: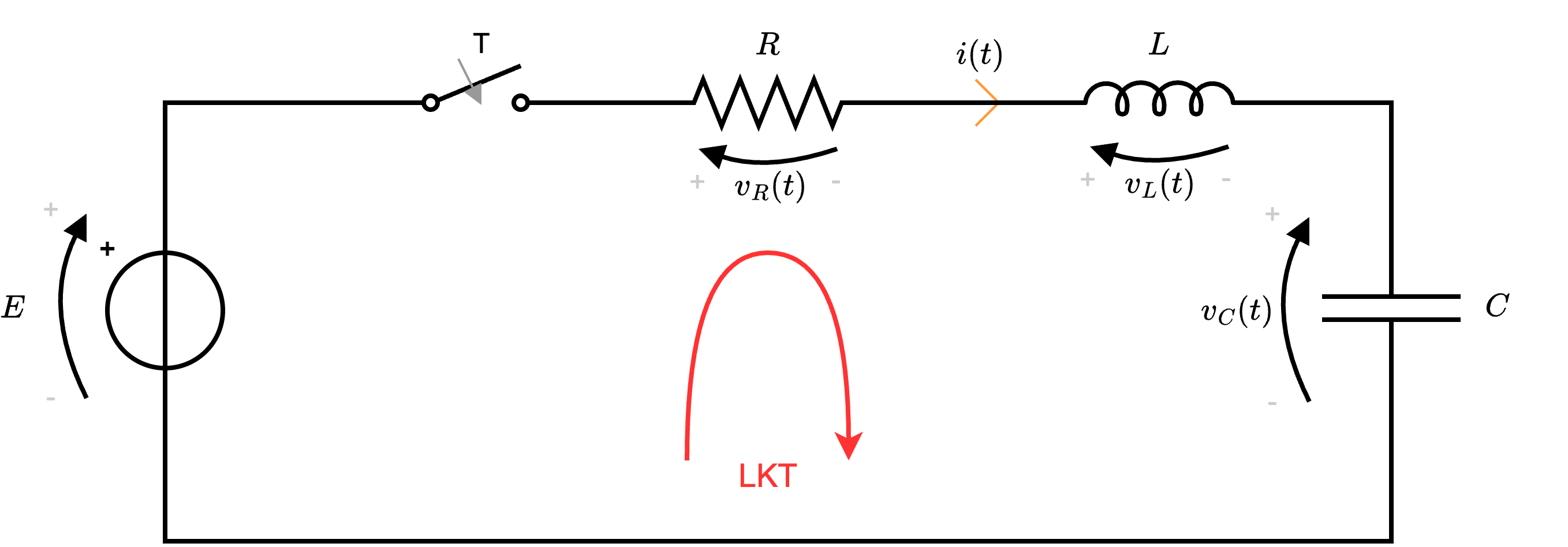 
da cui otteniamo la seguente equazione \[ LKT: \quad E - v_R(t) - v_L(t) - v_C(t) = 0 \] Considerando ora le equazioni costitutive dei componenti, ovvero \[ \left\{ \begin{array}{ccl} v_R(t) & = & R \cdot i(t) \\ v_L(t) & = & L \cdot \frac{d}{d t}i(t) \\ i(t) & = & C \cdot \frac{d}{d t}v_C(t) \end{array} \right. \qquad \implies \qquad \left\{ \begin{array}{ccl} v_R(t) & = & R \cdot i(t) \\ v_L(t) & = & L \cdot \frac{d}{d t}i(t) \\ \int i(t) \ dt & = & C \cdot v_C(t) \end{array} \right. \] si ha che è possibile ottenere le seguenti sostituzioni \[ \left\{ \begin{array}{ccl} v_R(t) & = & R \cdot i(t) \\ v_L(t) & = & L \cdot \frac{d}{d t}i(t) \\ v_C(t) & = & \frac{1}{C} \cdot \int i(t) \ dt \end{array} \right. \] Sostituendo all'equazione LKT, si ottiene \[ LKT: \quad E - R \cdot i(t) - L \cdot \frac{d}{d t}i(t) - \frac{1}{C} \cdot \int i(t) \ dt = 0 \] Derivando prima \[ LKT: \quad - R \cdot \frac{d}{d t} i(t) - L \cdot \frac{d^2}{d t}i(t) - \frac{1}{C} \cdot i(t) = 0 \] e riordinando poi \[ LKT: \quad \frac{d^2}{d t} i(t) + \frac{R}{L} \cdot \frac{d}{d t} i(t) + \frac{1}{L \cdot C} \cdot i(t) = 0 \] si ottiene un'equazione differenziale ordinaria omogenea a coefficienti costanti del secondo ordine, che è possibile risolvere utilizzando il metodo di Cauchy.
Considerando le ipotesi iniziali e il fatto che corrente e tensione siano variabili di stato, cioè \[ \begin{array}{c} v_C(t_0 = 0^-) = v_C(t_1 = 0) = v_{C0} i(t_0 = 0^-) = i(t_1 = 0) = 0 \end{array} \] si ha che si dovrà risolvere \[ \left\{ \begin{array}{l} \frac{d^2}{d t} i(t) + \frac{R}{L} \cdot \frac{d}{d t} i(t) + \frac{1}{L \cdot C} \cdot i(t) = 0 \\ v_C(0) = v_{C0} \\ i(0) = 0 \end{array} \right. \]
- il condensatore inizialmente ha una certa energia \( v_{C0}\), ovvero la tensione iniziale (all'istante \( t_0 = 0^-\)) del condensatore è uguale a \( v_{C0}\), cioè \[ v(t_0 = 0^-) = v_{C0} \]
- all'istante \( t_1 = 0\), l'interruttore T si chiude.
- la corrente che scorre inizialmente nel circuito è \( 0 \mathrm{ \, A }\), dato che il circuito è aperto, cioè \[ i(t_0 = 0^-) = 0 \mathrm{ \, A } \]
Corrente del circuito
Per risolvere questo circuito, consideriamo di applicare LKTConsiderando le ipotesi iniziali e il fatto che corrente e tensione siano variabili di stato, cioè \[ \begin{array}{c} v_C(t_0 = 0^-) = v_C(t_1 = 0) = v_{C0} i(t_0 = 0^-) = i(t_1 = 0) = 0 \end{array} \] si ha che si dovrà risolvere \[ \left\{ \begin{array}{l} \frac{d^2}{d t} i(t) + \frac{R}{L} \cdot \frac{d}{d t} i(t) + \frac{1}{L \cdot C} \cdot i(t) = 0 \\ v_C(0) = v_{C0} \\ i(0) = 0 \end{array} \right. \]
Risoluzione dell'equazione
Al fine di calcolare la soluzione, consideriamo il polinomio caratteristico associato (dato dalle incognite dello stesso grado del grado di derivazione) \[ \lambda^2 + \frac{R}{L} \cdot \lambda + \frac{1}{L \cdot C} = 0 \] che ha come soluzioni \[ \begin{array}{ccl} \lambda_{1, 2} & = & \frac{-\frac{R}{L} \pm \sqrt{\left( \frac{R}{L} \right)^2 - \frac{4}{L \cdot C}}}{2} \\ & = & -\frac{R}{2 \cdot L} \pm \frac{1}{2} \cdot \sqrt{\left( \frac{R}{L} \right)^2 - \frac{4}{L \cdot C}} \\ & = & -\frac{R}{2 \cdot L} \pm \frac{1}{2} \cdot \sqrt{\frac{1}{4} \cdot \left( \frac{R}{L} \right)^2 - \frac{4}{4 \cdot L \cdot C}} \\ & = & -\frac{R}{2 \cdot L} \pm \frac{1}{2} \cdot \sqrt{ \left( \frac{R}{2 \cdot L} \right)^2 - \frac{1}{L \cdot C}} \end{array} \] Definiamo quindi- il coefficiente di smorzamento \( \alpha\) uguale a \[ \alpha = \frac{R}{2 \cdot L} \]
- la pulsazione di risonanza \( (\omega_0)^2\) uguale a \[ (\omega_0)^2 = \frac{1}{L \cdot C} \]
Definizione - Circuiti RLC, caso \( \Delta \gt 0\) (risposta sovrasmorzata)
Nel caso in cui \( \Delta \gt 0\) (che implicherebbe \( \alpha \gt \omega_0\)) si hanno soluzioni reali distinte che si combinano nel seguente modo \[ i(t) = A \cdot \mathrm{e}^{\lambda_1 \cdot t} + B \cdot \mathrm{e}^{\lambda_2 \cdot t} \] Per calcolare i coefficienti consideriamo che si conosce il valore di \( i(0)\) ed è quindi possibile calcolare \[ \begin{array}{ccl} 0 & = & i(0) \\ & = & A \cdot \mathrm{e}^{\lambda_1 \cdot 0} + B \cdot \mathrm{e}^{\lambda_2 \cdot 0} \\ & = & A + B \end{array} \] che implica quindi \[ A = -B \] Considerando ora che conosciamo il valore di \( v_C(0)\) e il fatto che \( v_C(t)\) è uguale a \[ E - v_R(t) - v_L(t) - v_C(t) = 0 \qquad \implies \qquad v_C(t) = E - v_R(t) - v_L(t) \] è possibile ricavare il valore di \( \frac{d}{d t} i(0)\) dall'equazione \[ \begin{array}{ccl} v_{C0} & = & v_C(0) \\ & = & E - v_R(0) - v_L(0) \\ & = & E - R \cdot i(0) - L \cdot \frac{d}{d t} i(0) \\ & = & E - L \cdot \frac{d}{d t} i(0) \end{array} \] Risolvendola, si ottiene \[ v_{C0} = E - L \cdot \frac{d}{d t} i(0) \qquad \implies \qquad \frac{d}{d t} i(0) = \frac{E - v_{C0}}{L} \] Derivando la soluzione generica di \( i(t)\) si otterrebbe \[ \begin{array}{ccl} \frac{E - v_{C0}}{L} & = & \frac{d}{d t} i(0) \\ & = & \frac{d}{d t} \left[ A \cdot \mathrm{e}^{\lambda_1 \cdot t} + B \cdot \mathrm{e}^{\lambda_2 \cdot t} \right]_0 \\ & = & \left[ A \cdot \lambda_1 \cdot \mathrm{e}^{\lambda_1 \cdot t} + B \cdot \lambda_2 \cdot \mathrm{e}^{\lambda_2 \cdot t} \right]_0 \\ & = & A \cdot \lambda_1 \cdot \mathrm{e}^{\lambda_1 \cdot 0} + B \cdot \lambda_2 \cdot \mathrm{e}^{\lambda_2 \cdot 0} \\ & = & A \cdot \lambda_1 + B \cdot \lambda_2 \end{array} \] e risolvendo tale equazione \begin{aligned} & \frac{E - v_{C0}}{L} = A \cdot \lambda_1 + B \cdot \lambda_2 & \overset{B = -A}{\iff} \\ & \frac{E - v_{C0}}{L} = A \cdot \lambda_1 - A \cdot \lambda_2 & \iff \\ & \frac{E - v_{C0}}{L} = A \cdot (\lambda_1 - \lambda_2) & \iff \\ & \frac{E - v_{C0}}{L \cdot (\lambda_1 - \lambda_2)} = A & \iff \end{aligned} Si ha quindi che la corrente è uguale a \[ \begin{array}{ccl} i(t) & = & \frac{E - v_{C0}}{L \cdot (\lambda_1 - \lambda_2)} \cdot \mathrm{e}^{\lambda_1 \cdot t} - \frac{E - v_{C0}}{L \cdot (\lambda_1 - \lambda_2)} \cdot \mathrm{e}^{\lambda_2 \cdot t} \\ & = & \frac{E - v_{C0}}{L \cdot (\lambda_1 - \lambda_2)} \cdot \left( \mathrm{e}^{\lambda_1 \cdot t} - \mathrm{e}^{\lambda_2 \cdot t} \right) \\ & \overset{\text{sost.} \ \lambda_{1,2}}{=} & \frac{E - v_{C0}}{2 \cdot L \cdot \sqrt{\alpha^2 - (\omega_0)^2}} \cdot \left( \mathrm{e}^{\left(-\alpha + \sqrt{\alpha^2 - (\omega_0)^2}\right) \cdot t} - \mathrm{e}^{\left(-\alpha - \sqrt{\alpha^2 - (\omega_0)^2}\right) \cdot t} \right) \\ & = & \frac{E - v_{C0}}{2 \cdot L \cdot \sqrt{\alpha^2 - (\omega_0)^2}} \cdot \left( \mathrm{e}^{\sqrt{\alpha^2 - (\omega_0)^2} \cdot t} - \mathrm{e}^{-\sqrt{\alpha^2 - (\omega_0)^2} \cdot t} \right) \cdot \mathrm{e}^{-\alpha \cdot t} \end{array} \] che si grafica nel seguente modo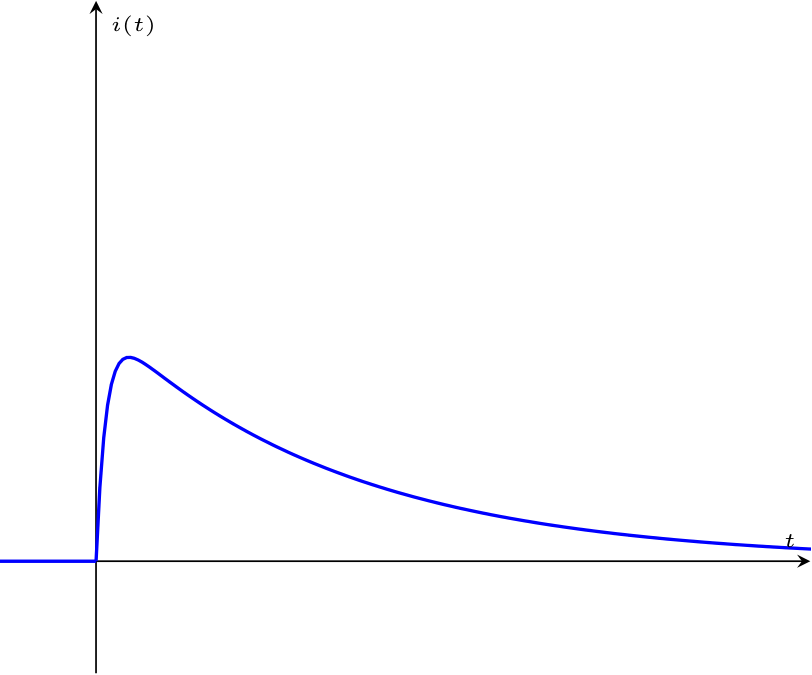 
Si dice che tale grafico rappresenta una risposta sovrasmorzata.
Definizione - Circuiti RLC, caso \( \Delta = 0\) (smorzamento critico)
Nel caso in cui \( \Delta = 0\) (che implicherebbe \( \alpha = \omega_0\)) si hanno soluzioni reali coincidenti che si combinano nel seguente modo \[ i(t) = A \cdot \mathrm{e}^{\lambda \cdot t} + B \cdot t \cdot \mathrm{e}^{\lambda \cdot t} \] Per calcolare i coefficienti consideriamo che si conosce il valore di \( i(0)\) ed è quindi possibile calcolare \[ \begin{array}{ccl} 0 & = & i(0) \\ & = & A \cdot \mathrm{e}^{\lambda \cdot 0} + B \cdot 0 \cdot \mathrm{e}^{\lambda_2 \cdot 0} \\ & = & A \end{array} \] che implica quindi \[ A = 0 \] Considerando ora che conosciamo il valore di \( v_C(0)\) e il fatto che \( v_C(t)\) è uguale a \[ E - v_R(t) - v_L(t) - v_C(t) = 0 \qquad \implies \qquad v_C(t) = E - v_R(t) - v_L(t) \] è possibile ricavare il valore di \( \frac{d}{d t} i(0)\) \[ \begin{array}{ccl} v_{C0} & = & v_C(0) \\ & = & E - v_R(0) - v_L(0) \\ & = & E - R \cdot i(0) - L \cdot \frac{d}{d t} i(0) \\ & = & E - L \cdot \frac{d}{d t} i(0) \end{array} \] Risolvendola, si ottiene \[ v_{C0} = E - L \cdot \frac{d}{d t} i(0) \qquad \implies \qquad \frac{d}{d t} i(0) = \frac{E - v_{C0}}{L} \] Derivando la soluzione generica di \( i(t)\) si otterrebbe \[ \begin{array}{ccl} \frac{E - v_{C0}}{L} & = & \frac{d}{d t} i(0) \\ & = & \frac{d}{d t} \left[ A \cdot \mathrm{e}^{\lambda \cdot t} + B \cdot t \cdot \mathrm{e}^{\lambda \cdot t} \right]_0 \\ & \overset{A = 0}{=} & \frac{d}{d t} \left[ B \cdot t \cdot \mathrm{e}^{\lambda \cdot t} \right]_0 \\ & = & \left[ B \cdot t \cdot \lambda \cdot \mathrm{e}^{\lambda \cdot t} + B \cdot \mathrm{e}^{\lambda \cdot t} \right]_0 \\ & = & B \cdot 0 \cdot \lambda \cdot \mathrm{e}^{\lambda \cdot 0} + B \cdot \mathrm{e}^{\lambda \cdot 0} \\ & = & B \end{array} \] ovvero \[ B = \frac{E - v_{C0}}{L} \] Si ha quindi che la corrente è uguale a \[ \begin{array}{ccl} i(t) & = & 0 \cdot \mathrm{e}^{\lambda \cdot t} + \frac{E - v_{C0}}{L} \cdot t \cdot \mathrm{e}^{\lambda \cdot t} \\ & = & \frac{E - v_{C0}}{L} \cdot t \cdot \mathrm{e}^{\lambda \cdot t} \end{array} \] che si grafica nel seguente modo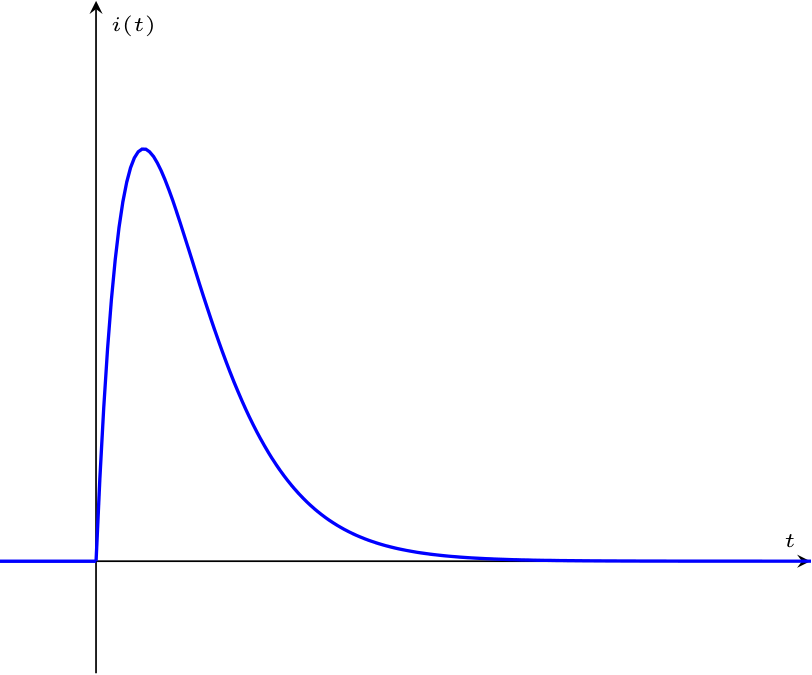 
Si dice che tale grafico rappresenta uno smorzamento critico.
Definizione - Circuiti RLC, caso \( \Delta \lt 0\) (risposta sottosmorzata)
Nel caso in cui \( \Delta \lt 0\) (che implicherebbe \( \alpha \lt \omega_0\)) si hanno soluzioni complesse coniugate, infatti le soluzioni sono uguali a \[ \begin{array}{ccl} \lambda_{1,2} & = & -\alpha \pm \sqrt{\alpha^2 - (\omega_0)^2} \\ & = & -\alpha \pm \sqrt{-1 \cdot \left((\omega_0)^2 - \alpha^2 \right)} \\ & \overset{\jmath = \sqrt{-1}}{=} & -\alpha \pm \jmath \cdot \sqrt{(\omega_0)^2 - \alpha^2} \end{array} \] Definendo ora \( \omega_D\) come \[ \omega_D = \sqrt{(\omega_0)^2 - \alpha^2} \] si ha che è possibile scrivere le due soluzioni come \[ \begin{array}{ccl} \lambda_1 & = & -\alpha + \jmath \cdot \omega_D \\ \lambda_2 & = & -\alpha - \jmath \cdot \omega_D \end{array} \] Queste due soluzioni, dovrebbero combinarsi nella forma \[ i(t) = A \cdot \mathrm{e}^{\lambda_1 \cdot t} + B \cdot \mathrm{e}^{\lambda_2 \cdot t} \] Si conosce già, tuttavia, il valore di \( A\) e \( B\) dal caso \( \Delta \gt 0\): vale infatti \[ \begin{array}{ccl} A & = & \frac{E - v_{C0}}{L \cdot (\lambda_1 - \lambda_2)} \\ B & = & -\frac{E - v_{C0}}{L \cdot (\lambda_1 - \lambda_2)} \end{array} \] e, sostituendo le soluzioni con il risultato ottenuto, si ottengono i coefficienti \[ \begin{array}{ccl} A & = & \frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \\ B & = & -\frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \end{array} \] Otteniamo che la corrente è uguale a \[ \begin{array}{ccl} i(t) & = & \frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \cdot \mathrm{e}^{(-\alpha + \jmath \cdot \omega_D) \cdot t} - \frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \cdot \mathrm{e}^{(-\alpha - \jmath \cdot \omega_D) \cdot t} \\ & = & \frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \cdot \left( \mathrm{e}^{(-\alpha + \jmath \cdot \omega_D) \cdot t} - \mathrm{e}^{(-\alpha - \jmath \cdot \omega_D) \cdot t} \right) \\ & = & \frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \cdot \left( \mathrm{e}^{\jmath \cdot \omega_D \cdot t} - \mathrm{e}^{- \jmath \cdot \omega_D \cdot t} \right) \cdot \mathrm{e}^{-\alpha \cdot t} \end{array} \] Ricordando ora la rappresentazione polare di un numero complesso, secondo cui \[ \mathrm{e}^{\jmath \cdot \theta} = \cos\left( \theta \right) + \jmath \cdot \sin\left( \theta \right) \] si ottiene \[ \begin{array}{ccl} i(t) & = & \frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \cdot \left( \mathrm{e}^{\jmath \cdot \omega_D \cdot t} - \mathrm{e}^{- \jmath \cdot \omega_D \cdot t} \right) \cdot \mathrm{e}^{-\alpha \cdot t} \\ & = & \frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \cdot \left( \cos\left( \omega_D \cdot t \right) + \jmath \cdot \sin(\omega_D \cdot t) - \cos\left( \omega_D \cdot t \right) + \jmath \cdot \sin(\omega_D \cdot t) \right) \cdot \mathrm{e}^{-\alpha \cdot t} \\ & = & \frac{E - v_{C0}}{L \cdot 2 \cdot \jmath \cdot \omega_D} \cdot \left( 2 \cdot \jmath \cdot \sin(\omega_D \cdot t) \right) \cdot \mathrm{e}^{-\alpha \cdot t} \\ & = & \frac{E - v_{C0}}{L \cdot \omega_D} \cdot \sin(\omega_D \cdot t) \cdot \mathrm{e}^{-\alpha \cdot t} \\ \end{array} \] che si grafica nel seguente modo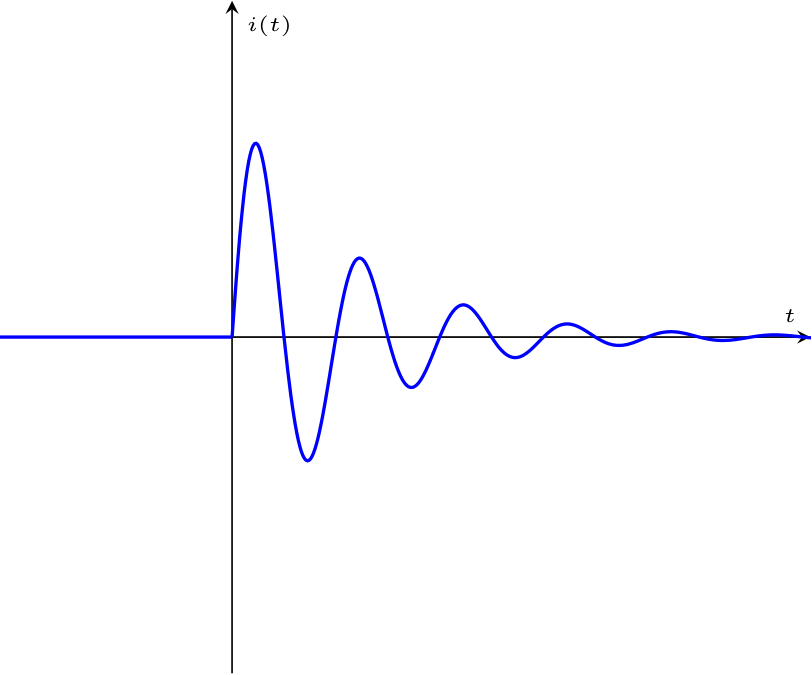 
Si dice che tale grafico rappresenta una risposta sottosmorzata.
Definizione - Metodo di risoluzione per ispezione
Una possibile strategia risolutiva per i circuiti caratterizzati da transitori, è utilizzare il metodo per ispezione che permette di conoscere il comportamento di corrente e tensione solo per alcuni istanti, ignorando il comportamento tenuto durante il transitorio.
In particolare è utile in circuiti di ordine superiore al primo, che sono caratterizzati da equazioni differenziali particolarmente complesse da risolvere. Quindi, dato un circuito caratterizzato dall'inizio di un transitorio all'istante \( t_0 = 0\) (dovuto, ad esempio, alla presenza di un interruttore \( T\) che modifica il suo stato), si considereranno solo alcuni istanti.
In particolare è utile in circuiti di ordine superiore al primo, che sono caratterizzati da equazioni differenziali particolarmente complesse da risolvere. Quindi, dato un circuito caratterizzato dall'inizio di un transitorio all'istante \( t_0 = 0\) (dovuto, ad esempio, alla presenza di un interruttore \( T\) che modifica il suo stato), si considereranno solo alcuni istanti.
Istante \( t_{0^-} = 0^-\)
Il primo istante che considereremo è \( t_{0^-} = 0^-\), in cui si considera il circuite a regime (ovvero è possibile sostituire condensatori e induttori con circuiti aperti e cortocircuiti) e la topologia del circuito non è influenzata dall'evento che scatenerà il transitorio (ad esempio, se all'istante \( t_0\) l'interruttore \( T\) si chiuderebbe, allora si considera l'interruttore aperto).Istante \( t_{0^+} = 0^+\)
Considereremo poi l'istante \( t_{0^+} = 0^+\), in cui ha inizio il transitorio. In questo caso, la topologia "ha subito" gli effetti dell'evento scatenante. Considerando però i componenti dinamici, si ha che le variabili di stato assumono lo stesso valore che avevano all'istante \( t_{0^-}\), per cui:- nel caso di condensatori, si ha che vale \[ v_C(t_{0^-}) = v_C(t_{0^+}) = v_{C0} \] e, per questo motivo, è possibile sostituirli con un generatore di tensione dello stesso valore Da notare che è mantenuta la convenzione dell'utilizzatore.
- nel caso di induttori, si ha che vale \[ i(t_{0^-}) = i(t_{0^+}) = I_{L0} \] e, per questo motivo, è possibile sostituirli con un generatore di corrente dello stesso valore Da notare che è mantenuta la convenzione dell'utilizzatore.
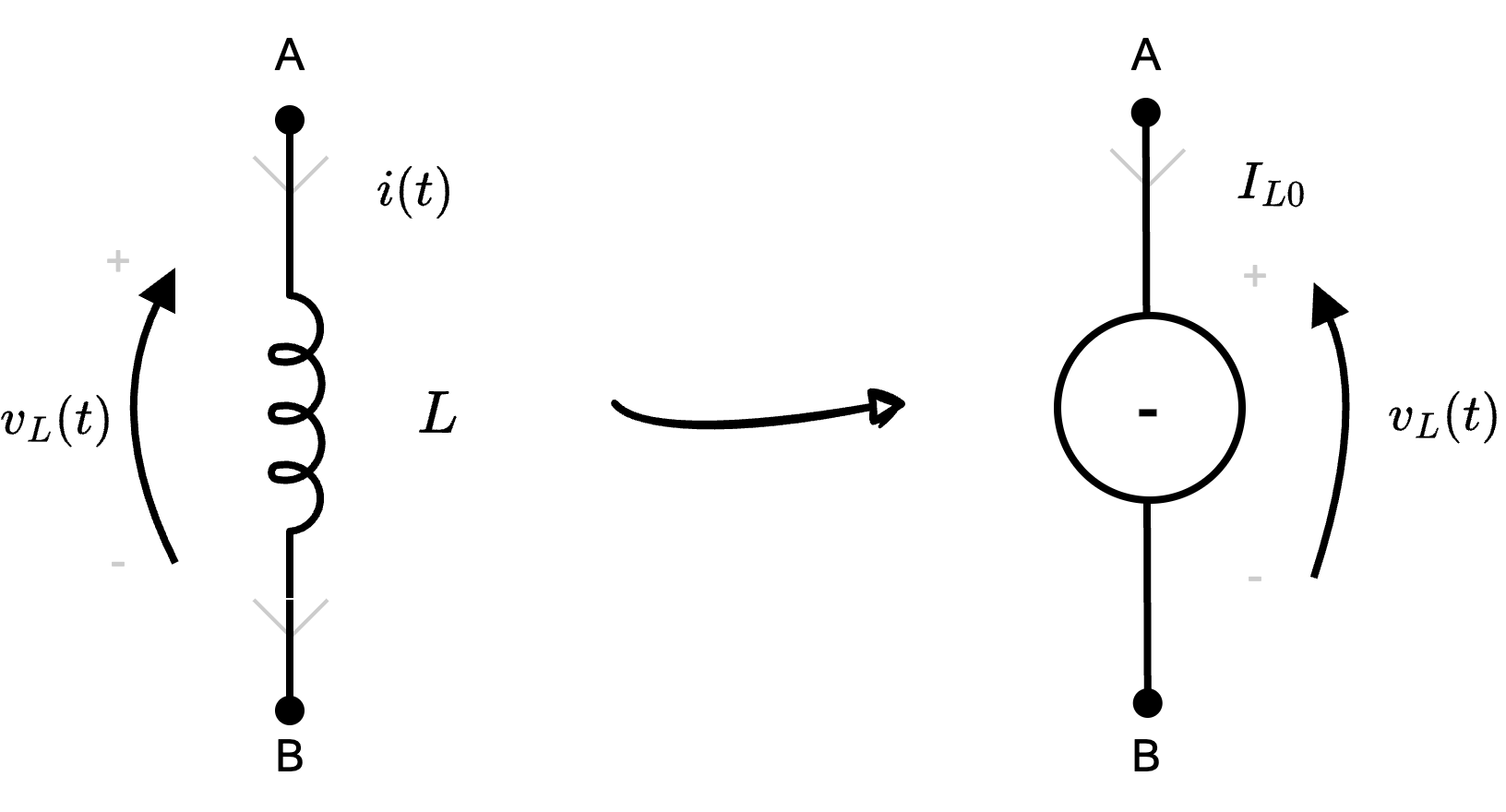
Istante \( t_{\infty} = +\infty\)
Infine si considera l'istante \( t_{\infty} = +\infty\), in cui il circuito è a regime (ed è possibile effettuare le relative sostituzioni). In questo caso, si ha che la topologia del circuito è influenzata dall'evento dell'istante \( t_0\).Esempio - Risoluzione di un circuito con il metodo dell'ispezione
Considerando il circuito 
e considerando che all'istante \( t_0 = 0\) l'interruttore \( T\) si chiude, calcolare: 
e, semplificandolo, si ottiene il seguente circuito 
A questo punto, oltre a calcolare i valori richiesti per l'istante \( t_{0^-}\), può essere utile calcolare tutti i valori delle variabili di stato, dato che serviranno per l'istante \( t_{0^+}\): infatti, per le variabili di stato, si ha che \( x(t_{0^-}) = x(t_{0^+})\).
Quindi, otteniamo che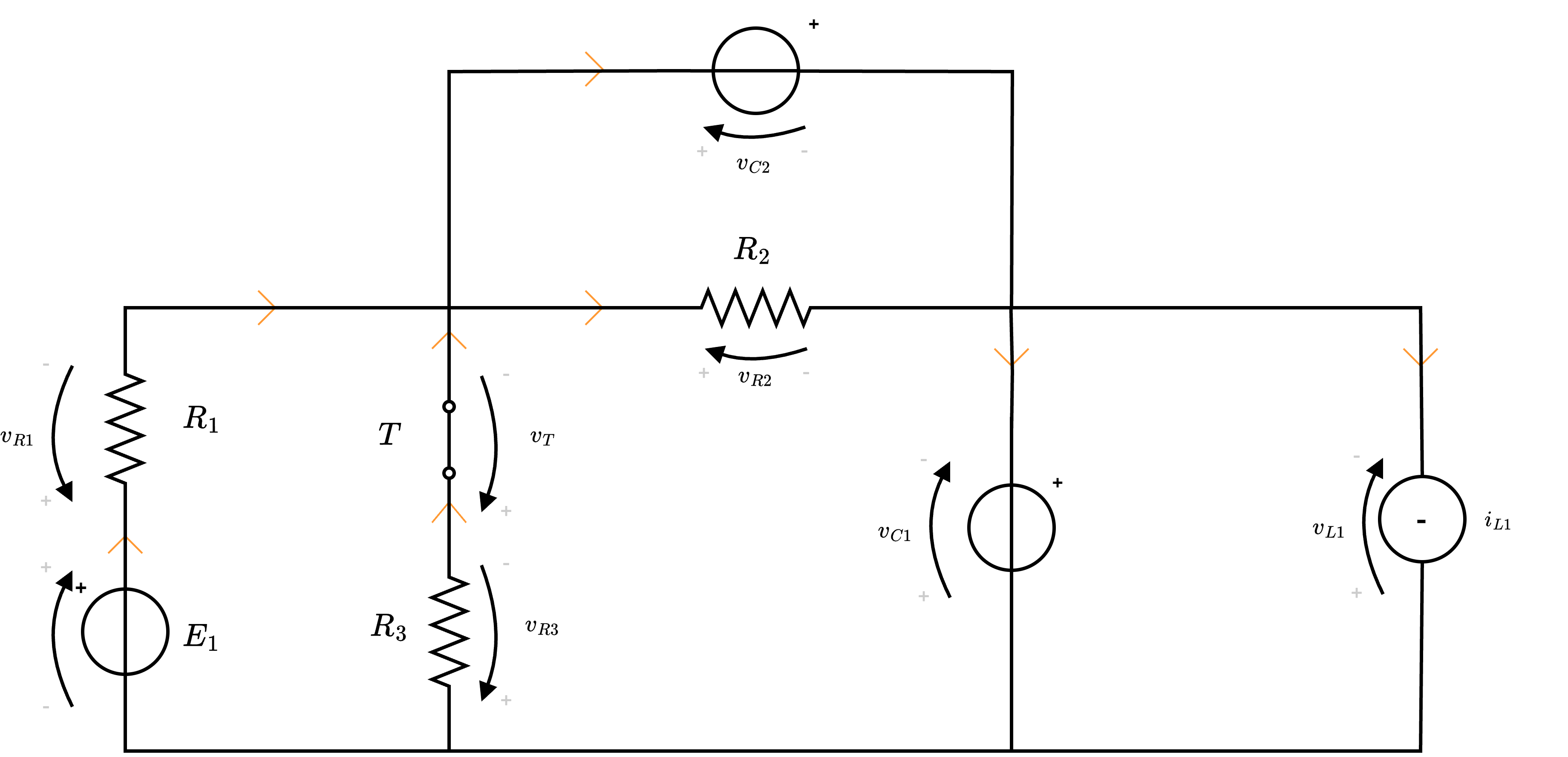
e 
e, semplificandolo, si ottiene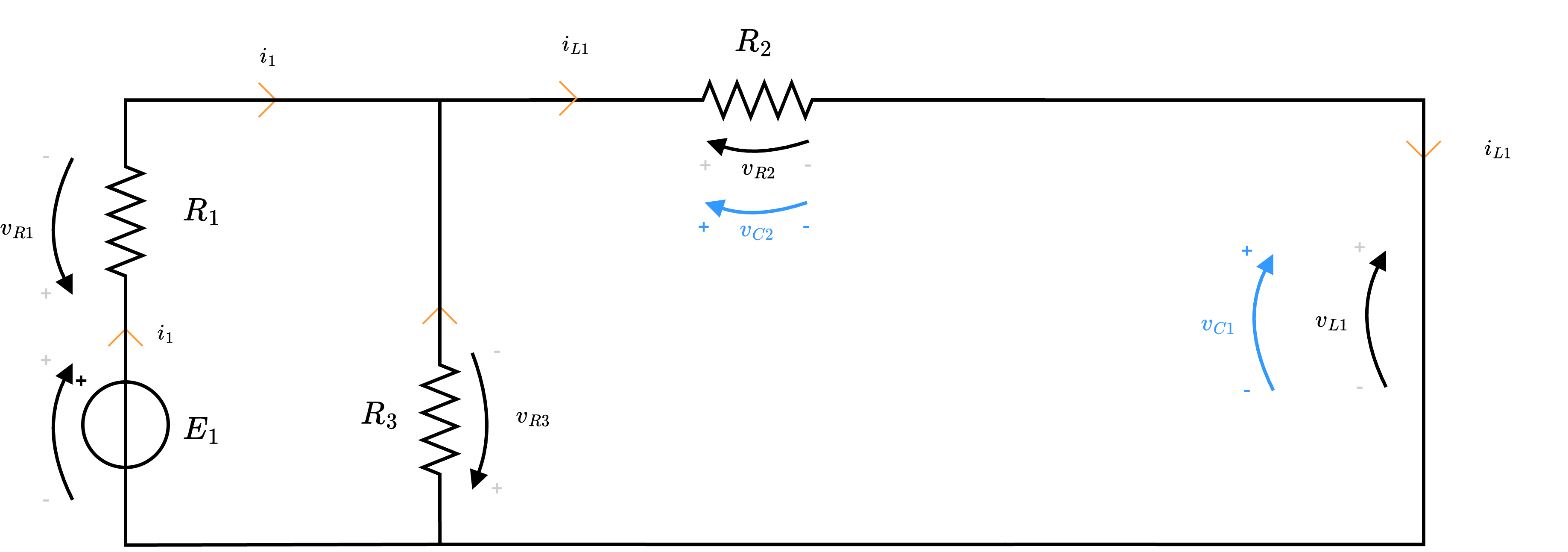 
Dato ciò, consideriamo che
- l'energia del condensatore \( C_2\) all'istante \( t_{0^-}\), ovvero \( w_{C2}(t_{0^-})\);
- la variazione della corrente sull'induttore \( L_1\) all'istante \( t_{0^+}\), ovvero \( \frac{d}{d t} i_L(t_{0^+})\);
- la potenza del generatore di tensione \( E_1\) all'istante \( t_{0^+}\), ovvero \( P_{E1}(t_{0^+})\);
- l'energia del condensatore \( C_1\) a regime, ovvero \( w_{C1}(\infty)\);
- l'energia del condensatore \( C_2\) a regime, ovvero \( w_{C2}(\infty)\);
- l'energia dell'induttore \( L_1\) a regime, ovvero \( w_{L1}(\infty)\).
Circuito orientato
Al fine calcolare tutti i valori richiesti, si ha che è utile orientare il circuitoIstante \( t_{0^-}\)
Considerando l'istante \( t_{0^-}\), si ha che il circuito si presenta nel seguente modoQuindi, otteniamo che
- la tensione \( v_{C1}(t_{0^-})\) è nulla (dato che è un cortocircuito), per cui \[ v_{C1}(t_{0^-}) = 0 \mathrm{ \, V } \]
- la corrente \( i_{L1}(t)\) è la stessa per tutto il circuito ed è uguale a \[ i_{L1}(t_{0^-}) = \frac{E_1}{R_1 + R_2} \] dato che la resistenza equivalente del circuito è l'equivalente alla serie delle due resistenze;
- la tensione \( v_{C2}(t_{0^-})\) è uguale alla tensione ai capi di \( R_2\), per cui data l'equazione costitutiva si ottiene \[ \begin{array}{ccl} v_{C2}(t_{0^-}) & = & v_{R2}(t_{0^-}) \\ & = & R \cdot i(t_{0^-}) \\ & = & R_2 \cdot i_L(t_{0^-}) \\ & = & R_2 \cdot \frac{E_1}{R_1 + R_2} \end{array} \]
Istante \( t_{0^+}\)
Considerando l'istante \( t_{0^+}\), si ha che il circuito si presenta nel seguente modo- per calcolare \( \frac{d}{d t} i_L(t_{0^+})\) è possibile considerare l'equazione costitutiva di \( L_1\), ovvero \[ v_{L1}(t_{0^+}) = L \cdot \frac{d}{d t} i_L(t_{0^+}) \qquad \implies \qquad \frac{d}{d t} i_L(t_{0^+}) = \frac{v_{L1}(t_{0^+})}{L} \] Per conoscere \( v_{L1}(t_{0^+})\) è ora possibile applicare LKT da cui è possibile calcolare \[ LKT: \quad v_{C1}(t_{0^+}) - v_{L1}(t_{0^+}) = 0 \qquad \implies \qquad v_{C1}(t_{0^+}) = v_{L1}(t_{0^+}) = 0 \mathrm{ \, V } \] e, dato che \( v_{C1}(t_{0^-}) = 0 \mathrm{ \, V }\) ed è una variabile di stato (ndr, proprio perchè la tensione dell'induttore non è una variabile di stato non la si è calcolata a \( t_{0^-}\)), si ha che \[ \begin{array}{ccl} \frac{d}{d t} i_L(t_{0^+}) & = & \frac{v_{L1}(t_{0^+})}{L} \\ & = & 0 \frac{\mathrm{ \, A }}{\mathrm{ \, s }} \end{array} \]
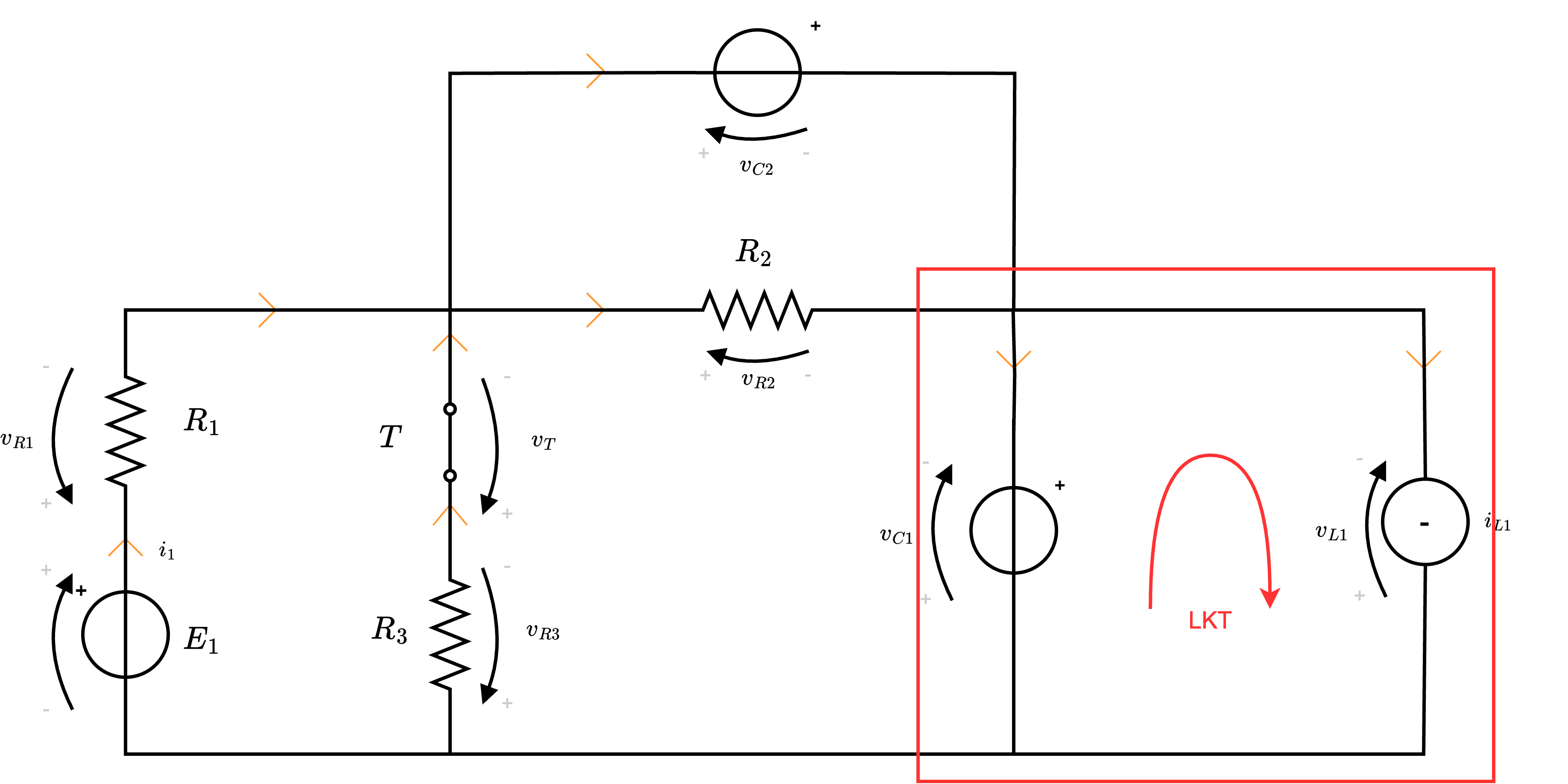
- per calcolare \( P_{E1}(t_{0^+})\) si ha che occorre calcolare \( i_1(t_{0^+})\) \[ P_{E1}(t_{0^+}) = E_1 \cdot i_1(t_{0^+}) \] e, per farlo, consideriamo di applicare LKT alla seguente maglia (ndr, scelta per convenienza dato che conosciamo già tutti i valori delle tensioni e \( R_1\) ha la stessa corrente di \( E_1\)) ottenendo \[ LKT: \quad E_1 - \overbrace{v_{R1}(t_{0^+})}^{R_1 \cdot i_1(t_{0^+})} - v_{C2}(t_{0^+}) - v_{C1}(t_{0^+}) = 0 \qquad \implies \qquad i_1(t_{0^+}) = \frac{v_{C2}(t_{0^+}) + v_{C1}(t_{0^+}) - E_1}{-R_1} \] e, ricordando che \( v_{C1}(t_{0^+}) = 0 \mathrm{ \, V }\), si ha che \[ i_1(t_{0^+}) = \frac{E_1 - v_{C2}(t_{0^+})}{R_1} \] si ha che \( P_{E1}(t_{0^+})\) è uguale a \[ P_{E1}(t_{0^+}) = E_1 \cdot \frac{E_1 - v_{C2}t_{0^+}}{R_1} \]
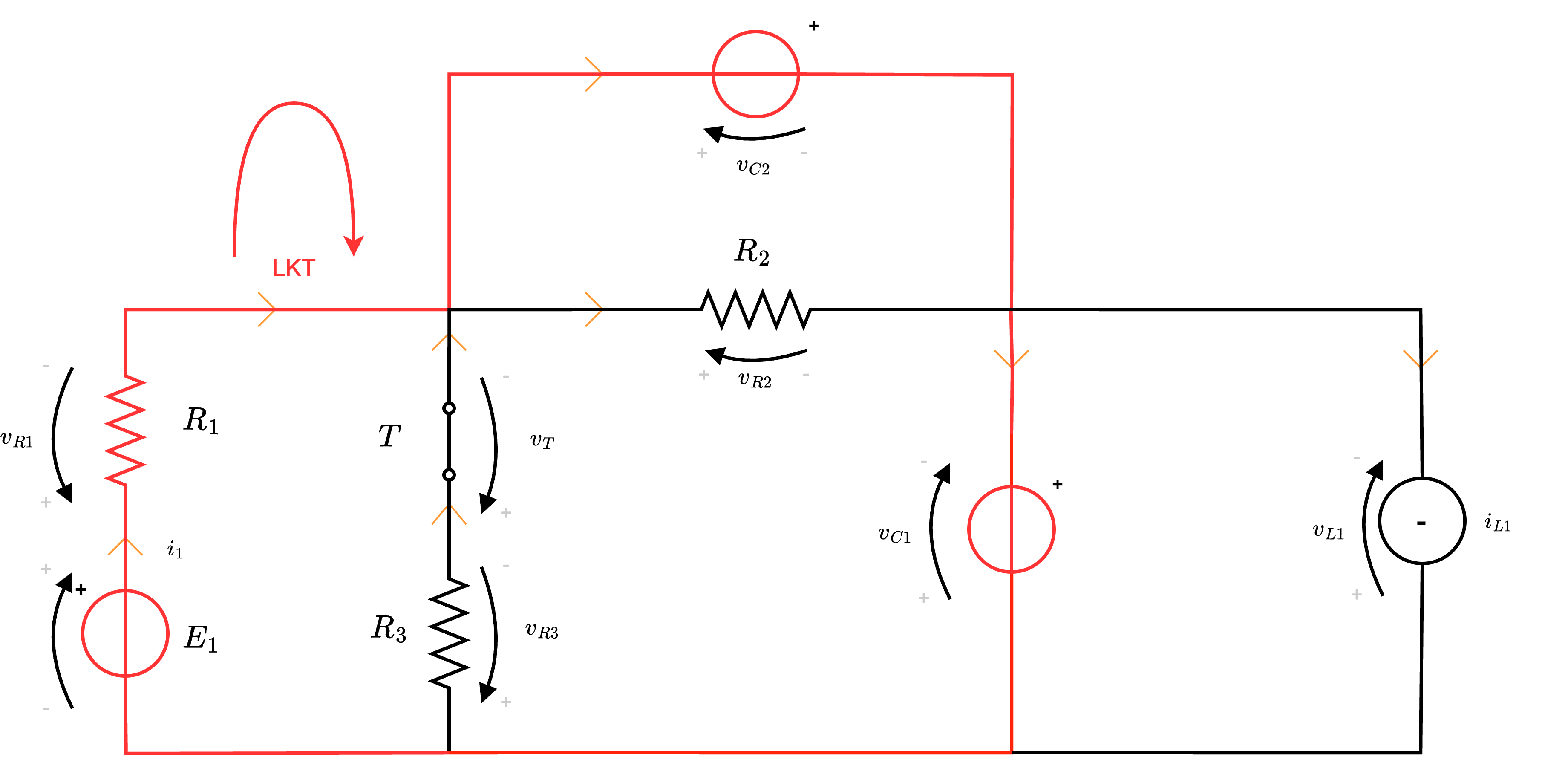
Istante \( t_\infty\)
Considerando il circuito a regime (ovvero all'istante \( t_\infty\)), si ha che si presenta nel seguente modo- per calcolare \( w_{C1}(t_\infty)\) consideriamo che \( v_{C1}(\infty) = 0 \mathrm{ \, V }\) (dato che è un cortocircuito) e quindi \[ \begin{array}{ccl} w_{C1}(t_\infty) & = & \frac{1}{2} \cdot C_1 \cdot \overbrace{\left( v_{C1}(t_\infty) \right)^2}^{0 \mathrm{ \, V }} \\ & = & 0 \mathrm{ \, V } \end{array} \]
- per calcolare \( w_{L1}(t_\infty)\) si utilizza la formula \[ w_{L1}(\infty) = \frac{1}{2} \cdot L_1 \cdot \left( i_L(t_\infty) \right)^2 \] Occorre quindi calcolare la corrente \( i_L(t_\infty)\): è possibile utilizzare la formula del partitore di corrente ottenendo \[ \begin{array}{ccl} i_{L1}(t_\infty) & = & \frac{R_{eq}}{R_2} \cdot i_1(t_\infty) \\ & = & \frac{R_2 \ // \ R_3}{R_2} \cdot \frac{E_1}{R_1} \\ & = & \frac{\frac{R_2 \cdot R_3}{R_2 + R_3}}{R_2} \cdot \frac{E_1}{R_1} \\ & = & \frac{R_3}{R_2 + R_3} \cdot \frac{E_1}{R_1} \end{array} \] da cui \[ \begin{array}{ccl} w_{L1}(\infty) & = & \frac{1}{2} \cdot L_1 \cdot \left( i_L(t_\infty) \right)^2 \\ & = & \frac{1}{2} \cdot L_1 \cdot \left( \frac{R_3}{R_2 + R_3} \cdot \frac{E_1}{R_1} \right)^2 \end{array} \]
- per calcolare \( w_{C2}(\infty)\) si utilizza la formula \[ w_{C2}(\infty) = \frac{1}{2} \cdot C_2 \cdot \left( v_{C2}(t_\infty) \right)^2 \] Occorre quindi calcolare \( v_{C2}(\infty)\) che è uguale a \( v_{R2}(\infty)\) ed è quindi uguale a \[ \begin{array}{ccl} v_{C2}(\infty) & = & v_{R2}(\infty) \\ & = & R_2 \cdot i_{L1}(\infty) \\ & = & R_2 \cdot \left( \frac{R_3}{R_2 + R_3} \cdot \frac{E_1}{R_1} \right) \end{array} \]