Definizione - Circuito elettrico
Un circuito elettrico è un insieme interconnesso di componenti elettrici (detti multipoli) e di loro collegamenti in un percorso chiuso in modo che la corrente elettrica possa fluire con continuità.
È possibile rappresentare un generico circuito come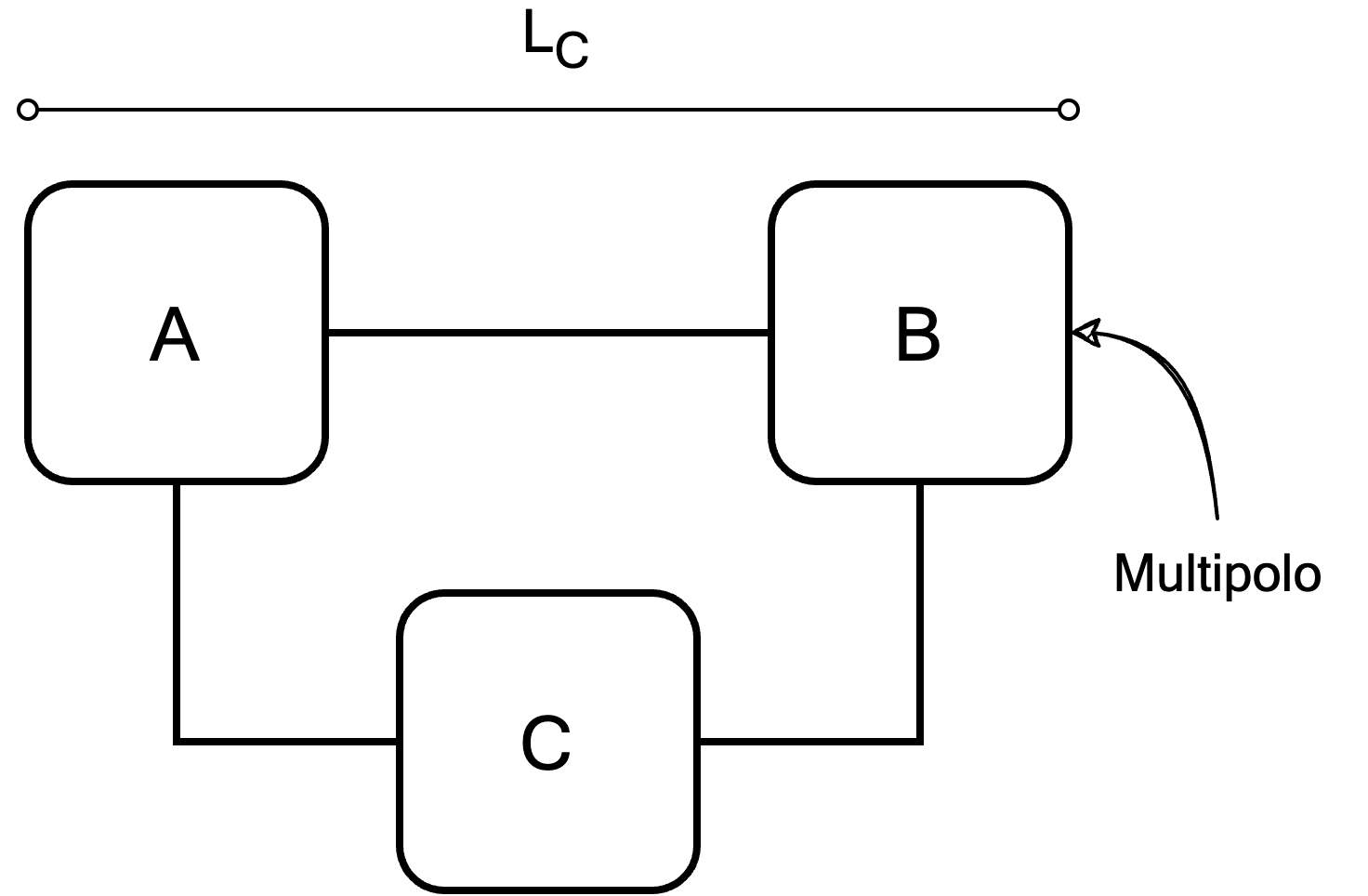
È possibile rappresentare un generico circuito come
Definizione - Ipotesi di confinamento dei fenomeni
I fenomeni elettromagnetici risultano confinati all'interno del circuito, ovvero all'esterno non vi è propagazione delle onde, per cui \[ \frac{\partial \underline{B}}{\partial t} = 0 \qquad \text{e} \qquad \frac{\partial \underline{D}}{\partial t} = 0 \]
Definizione - Ipotesi di quasi stazionarietà
Considerando
Sotto questa ipotesi, è possibile considerare i circuiti a parametri concentrati, ovvero è possibile trascurare la geometria del circuito e considerare solamente la topologia (si considera il circuito come un unico elemento).
- \( L_c\) la lunghezza di un circuito;
- \( \lambda\) la lunghezza d'onda del segnale. Si definisce \( \lambda\) uguale a \[ \lambda = \frac{\mathrm{c}}{f} \] dove
- \( \mathrm{c}\) è la velocità di propagazione nel mezzo (consideriamo la velocità della luce nel vuoto, pari circa a \( 300 000 \frac{\mathrm{ \, km }}{\mathrm{ \, s }}\));
- \( f\) è la frequenza.
Sotto questa ipotesi, è possibile considerare i circuiti a parametri concentrati, ovvero è possibile trascurare la geometria del circuito e considerare solamente la topologia (si considera il circuito come un unico elemento).
Nota bene - Ad esempio
Consideriamo il caso della rete elettrica, dove si ha:
- una frequenza \( f\) pari a \( 50 \mathrm{ \, Hz }\);
- una lunghezza (ipotetica) del circuito \( L_c\) pari a \( 10 \mathrm{ \, m }\)
Definizione - Elementi circuitali
Consideriamo un circuito composto da bipoli (multipoli con solo 2 estremità) più simile a quelli che saranno poi trattati 
In questo, identifichiamo: 
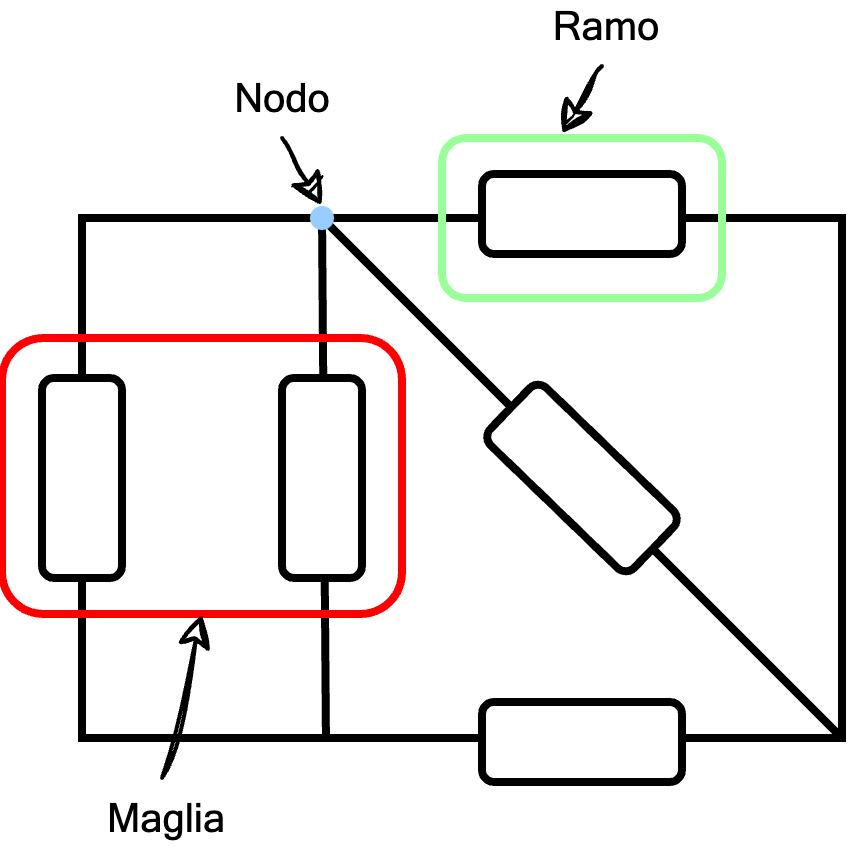
- i rami, ovvero i componenti con i loro terminali;
- i nodi, ovvero dei punti di congiunzione di due o più rami;
- le maglie, ovvero un percorso chiuso formato dai rami.
Definizione - Potenza elettrica
La potenza elettrica \( p(t)\) (misurata in Watt \( \mathrm{ \, W }\)) è una grandezza calcolabile come \[ p(t) = v(t) \cdot i(t) \] dove
- \( v(t)\) è la tensione, misurata in Volt \( \mathrm{ \, V }\);
- \( i(t)\) è l'intensità di corrente, misurata in Ampere \( \mathrm{ \, A }\).
Definizione - Energia
Considerando la potenza elettrica \( p(t)\), si ha che l'energia \( w(t)\) (misurata in Joule \( \mathrm{ \, J }\)) è uguale a \[ w(t) = \int_{t_1}^{t_2} p(\tau) \ d\tau \]
Definizione - Convenzione dell'utilizzatore e convenzione del generatore
Considerando la rappresentazione di un generico circuito, si ha che è "colui che legge" a stabilire il verso della corrente.
Per indicare la posizione del polo positivo o negativo, si utilizza una freccia indicante la tensione, nel seguente modo
ovvero la testa della freccia indica il polo positivo, mentre la coda indica il polo negativo.
È possibile adottare le seguenti convenzioni:
Per indicare la posizione del polo positivo o negativo, si utilizza una freccia indicante la tensione, nel seguente modo
È possibile adottare le seguenti convenzioni:
- la convenzione dell'utilizzatore prevede che la corrente "entri" dal terminale positivo (ed "esca" dal negativo), ovvero In questo caso, se la potenza è positiva (\( p(t) \gt 0\)) si dice che il componente assorbe potenza, altrimenti si dice che il componente genera;
- la convenzione del generatore prevede che la corrente "esca" dal terminale positivo (ed "entri" dal negativo), ovvero In questo caso, se la potenza è positiva (\( p(t) \gt 0\)) si dice che il componente genera potenza, altrimenti si dice che il componente assorbe;
Definizione - Risoluzione di un circuito
Risolvere un circuito significa calcolare tensioni e correnti di tutti i rami del circuito. Per farlo si utilizzano:
- le leggi di Kirchhoff, ovvero equazioni topologiche (che dipendono solo da come sono collegati i componenti, e non dai componenti stessi);
- le equazioni costitutive, che descrivono i componenti.
Dimostrazione - Legge di Kirchhoff per le tensioni (LKT)
Data la proposizione
Enunciato:
Considerando una maglia, la sommatoria delle tensioni di tutti i componenti è nulla, ovvero \[ \sum_{i = 1}^{\# \text{componenti}} v_i(t) = 0 \qquad \forall t \]
Dimostrazione:
Considerando la premessa che \[ \underset{l}{\oint} \underline{E} \ d\underline{l} = - \underset{S}{\iint} \frac{\partial \underline{B}}{\partial t} \bullet \hat{n} \ d\underline{S} \] Dato che per ipotesi \[ \frac{\partial \underline{B}}{\partial t} = 0 \] si ha che \[ \underset{l}{\oint} \underline{E} \ d\underline{l} = 0 \] Considerando inoltre (da premessa) che \( \underline{E}\) è conservativo, si ha che su una linea chiusa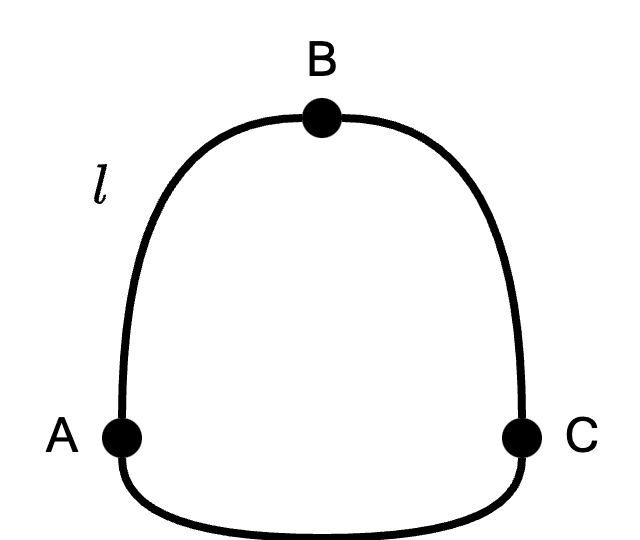 
si ha che \[ \overbrace{\underset{l}{\oint} \underline{E} \ d\underline{l}}^{0} \overbrace{=}^{\text{È conservativo}} \overbrace{\int_A^B \underline{E} \ d\underline{l}}^{v_{AB}} + \overbrace{\int_B^C \underline{E} \ d\underline{l}}^{v_{BC}} + \overbrace{\int_C^A \underline{E} \ d\underline{l}}^{v_{AC}} \] e quindi \[ v_{AB} + v_{BC} + v_{AC} = 0 \] che dimostra la legge.
Esempio - Calcolare le equazioni topologiche LKT
Considerando il seguente circuito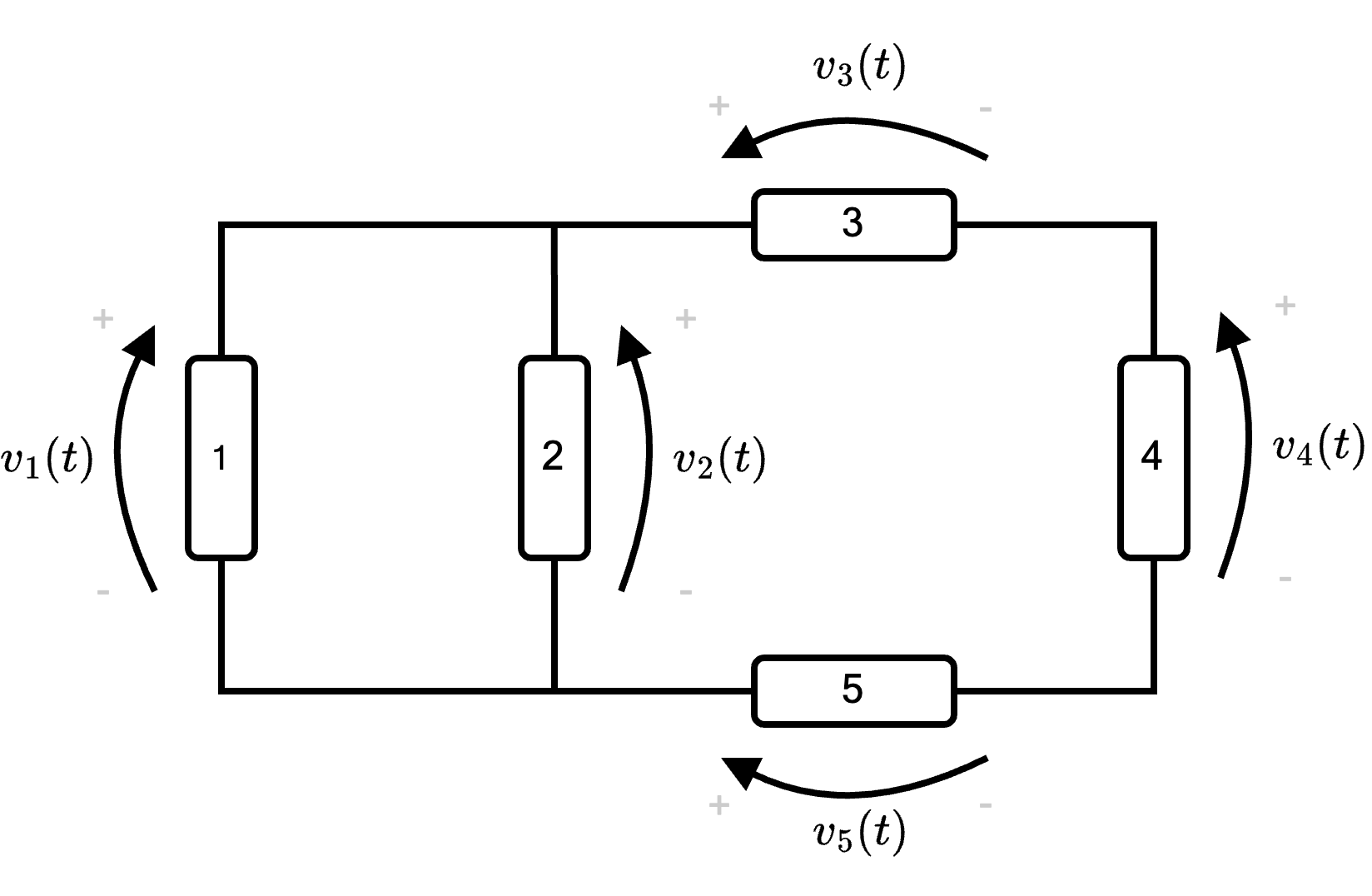 
per determinare le equazioni delle tensioni, è necessario identificare le maglie presenti:
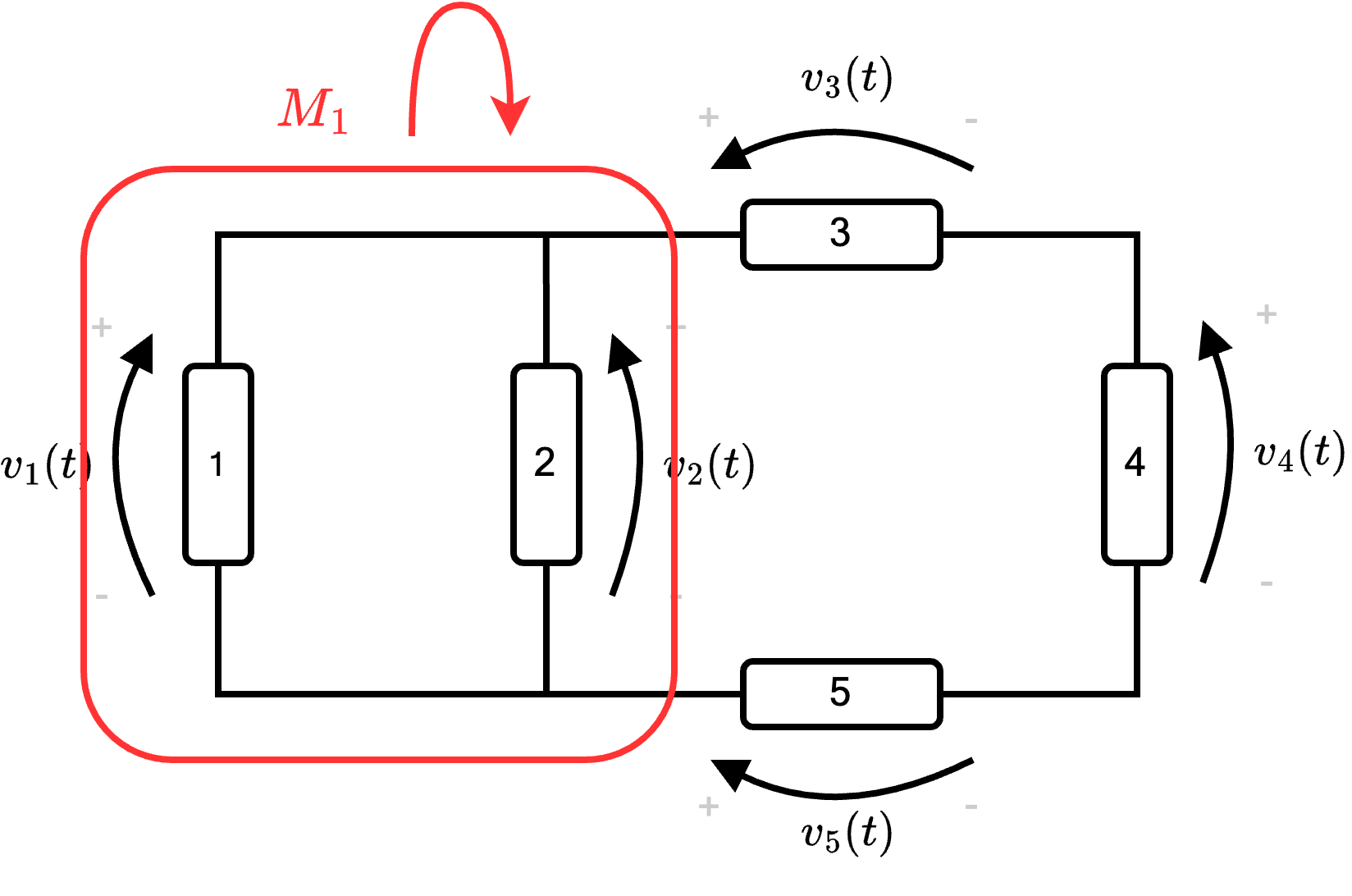
- consideriamo la maglia \( M_1\) determinando un verso di percorrenza (orario o antiorario). Per determinare l'equazione, assegniamo segno positivo alle tensioni di verso concorde (al verso scelto), mentre segno negativo alle tensioni con verso discorde. Otteniamo quindi l'equazione \[ M_1 \quad : \qquad v_1 - v_2 = 0 \]
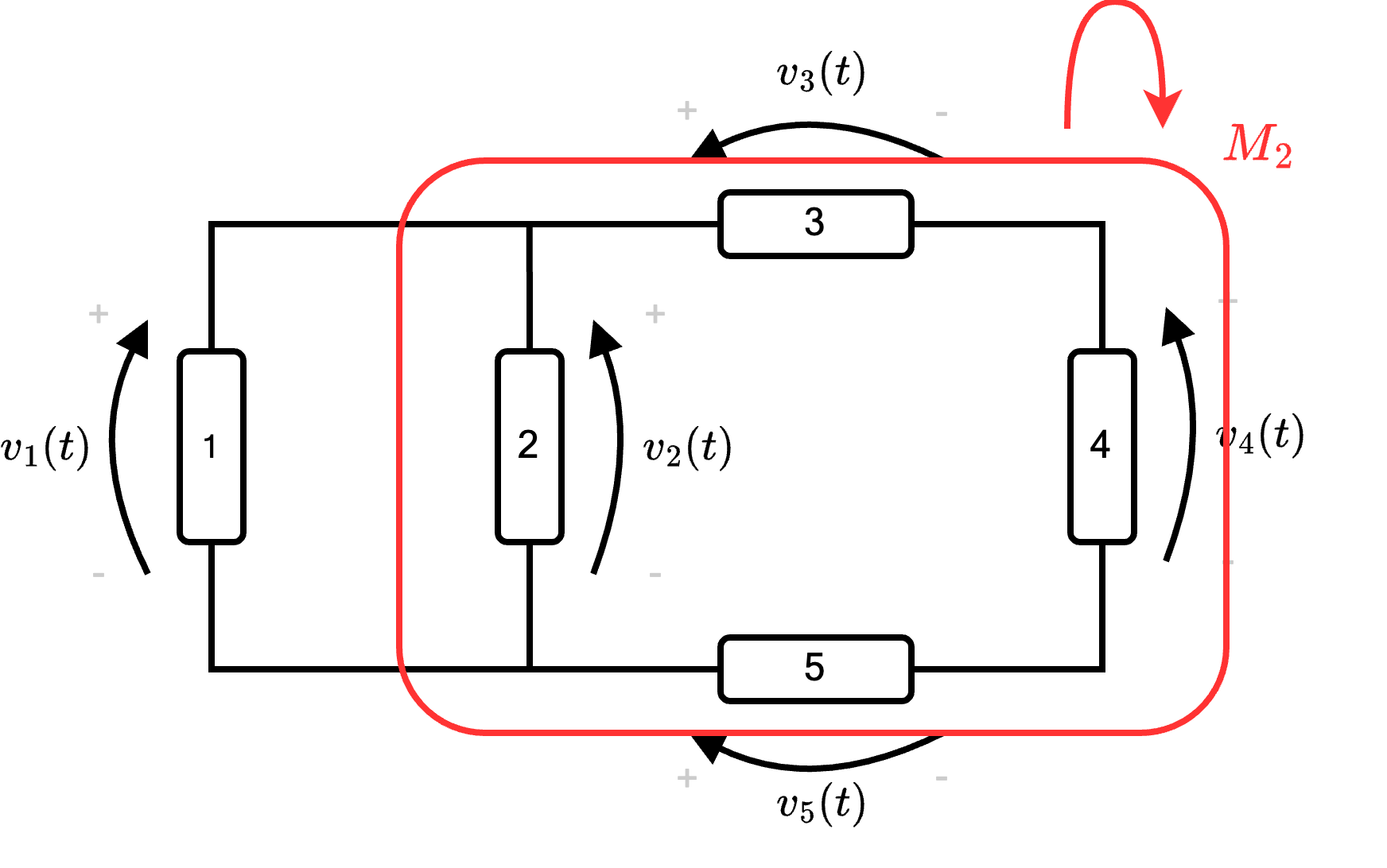
- consideriamo la maglia \( M_2\) e otteniamo l'equazione \[ M_2 \quad : \qquad v_2 - v_3 - v_4 + v_5 = 0 \]
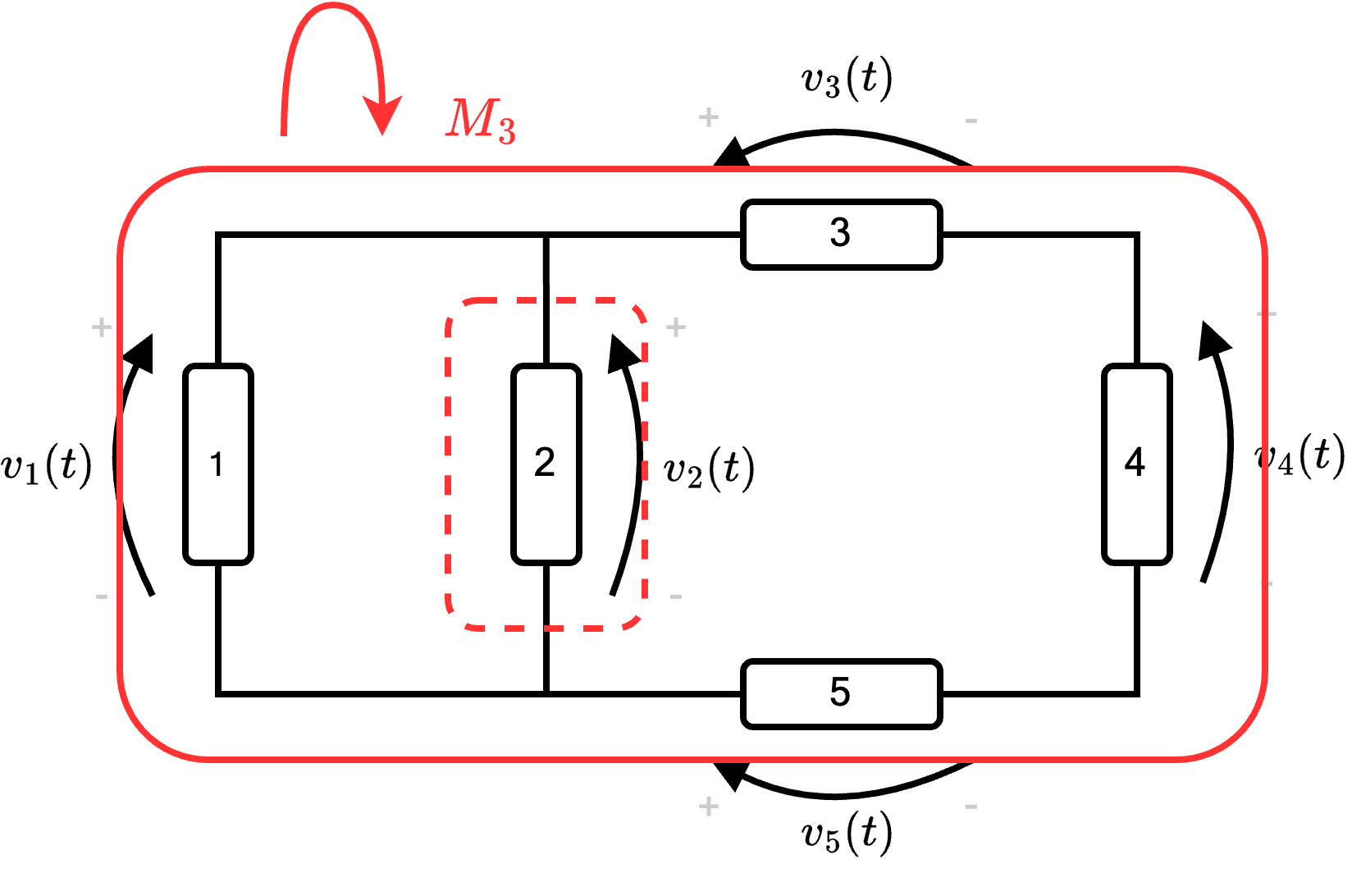
- consideriamo la maglia \( M_3\) (da notare che ignoriamo il componente \( v_2\), che non fa parte della maglia) e otteniamo l'equazione \[ M_3 \quad : \qquad v_1 - v_3 - v_4 + v_5 = 0 \]
Dimostrazione - Legge di Kirchhoff per le correnti (LKC)
Data la proposizione
Enunciato:
Considerando una superficie chiusa (ad esempio i nodi), la sommatoria delle correnti entranti è uguale alla sommatoria delle correnti uscenti, ovvero \[ \sum_{j = 1}^{\# \text{entranti}} i_j(t) = \sum_{k = 1}^{\# \text{uscenti}} i_k(t) \qquad \forall t \] o, in maniera equivalente (considerando i segni) \[ \sum_{j = 1}^{\# \text{correnti}} \pm i_j(t) = 0 \qquad \forall t \]
Dimostrazione:
Considerando la premessa che \[ \underset{S}{\iint} \left( \underline{J} + \frac{\partial \underline{D}}{\partial t} \right) \bullet \hat{n} \ d\underline{S} = 0 \] Dato che per ipotesi abbiamo che se \( S\) non interseca alcun componente \[ \frac{\partial \underline{D}}{\partial t} = 0 \] si ha che \[ \underset{S}{\iint} ( \underline{J} + \overbrace{\frac{\partial \underline{D}}{\partial t}}^{0} ) \ \bullet \ \hat{n} \ d\underline{S} = 0 \] e quindi \[ \underset{S}{\iint} \underline{J} \bullet \hat{n} \ d\underline{S} = 0 \] che dimostra la legge.
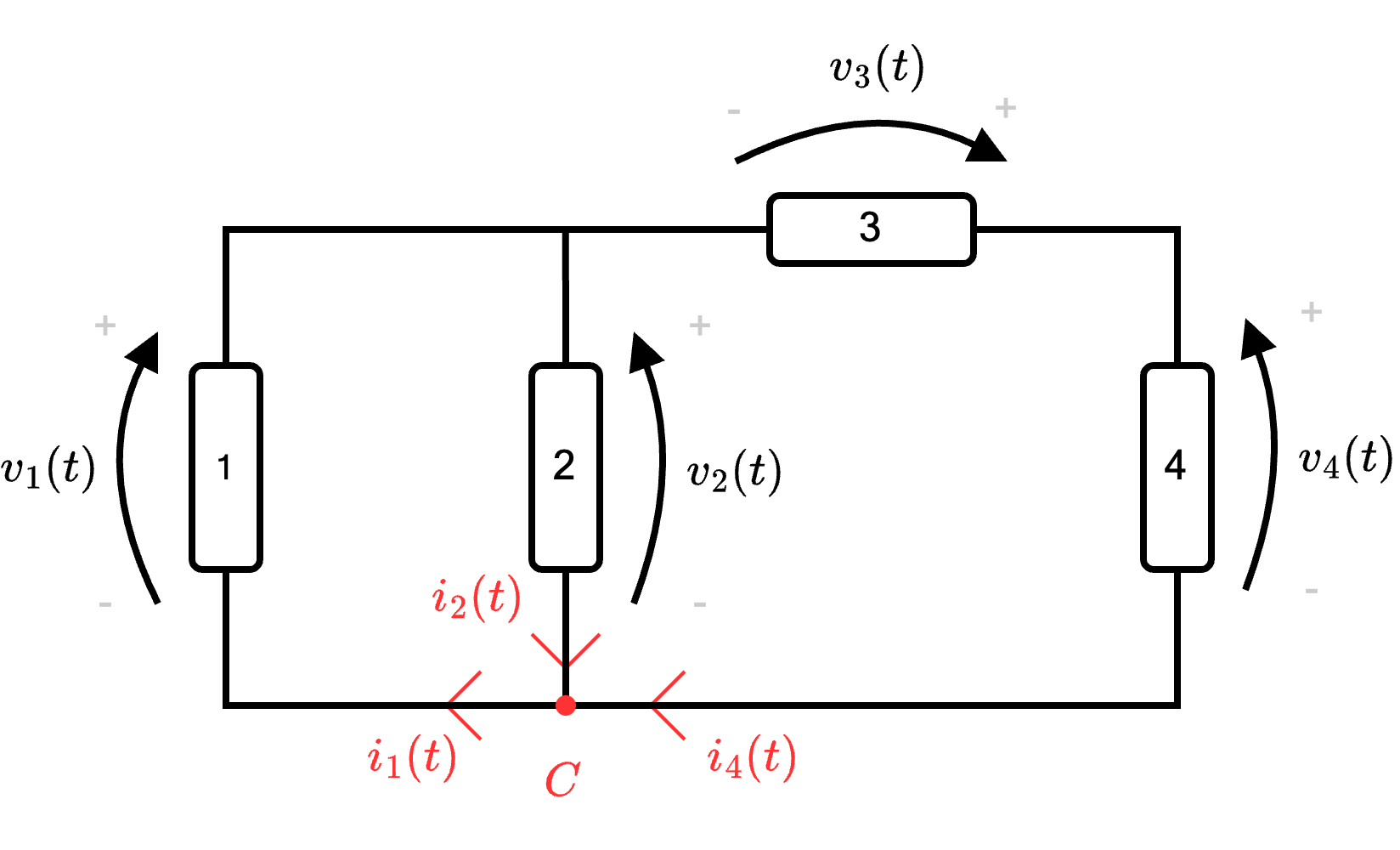
Esempio - Calcolare le equazione topologiche LKC
Considerando il seguente circuito 
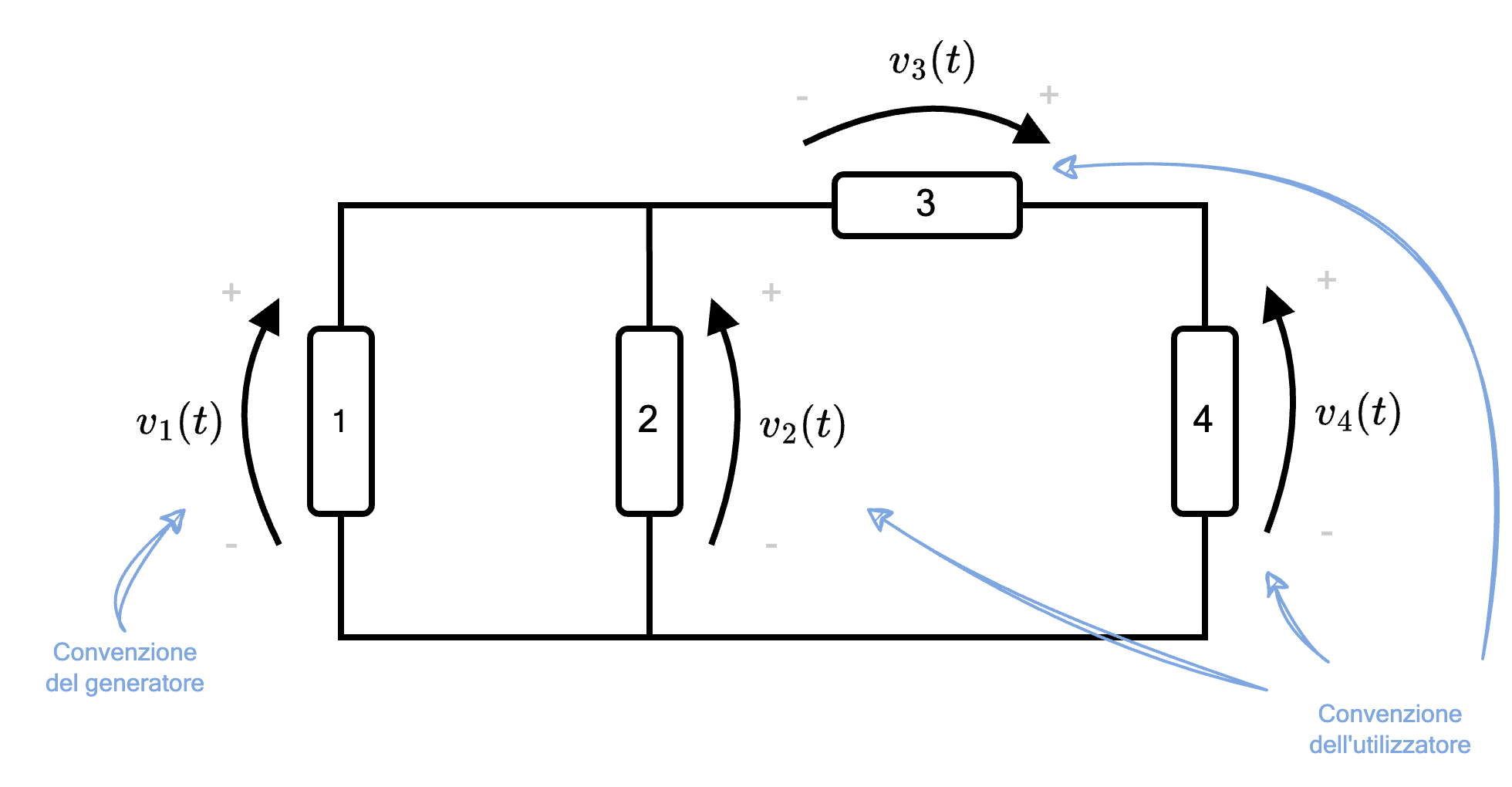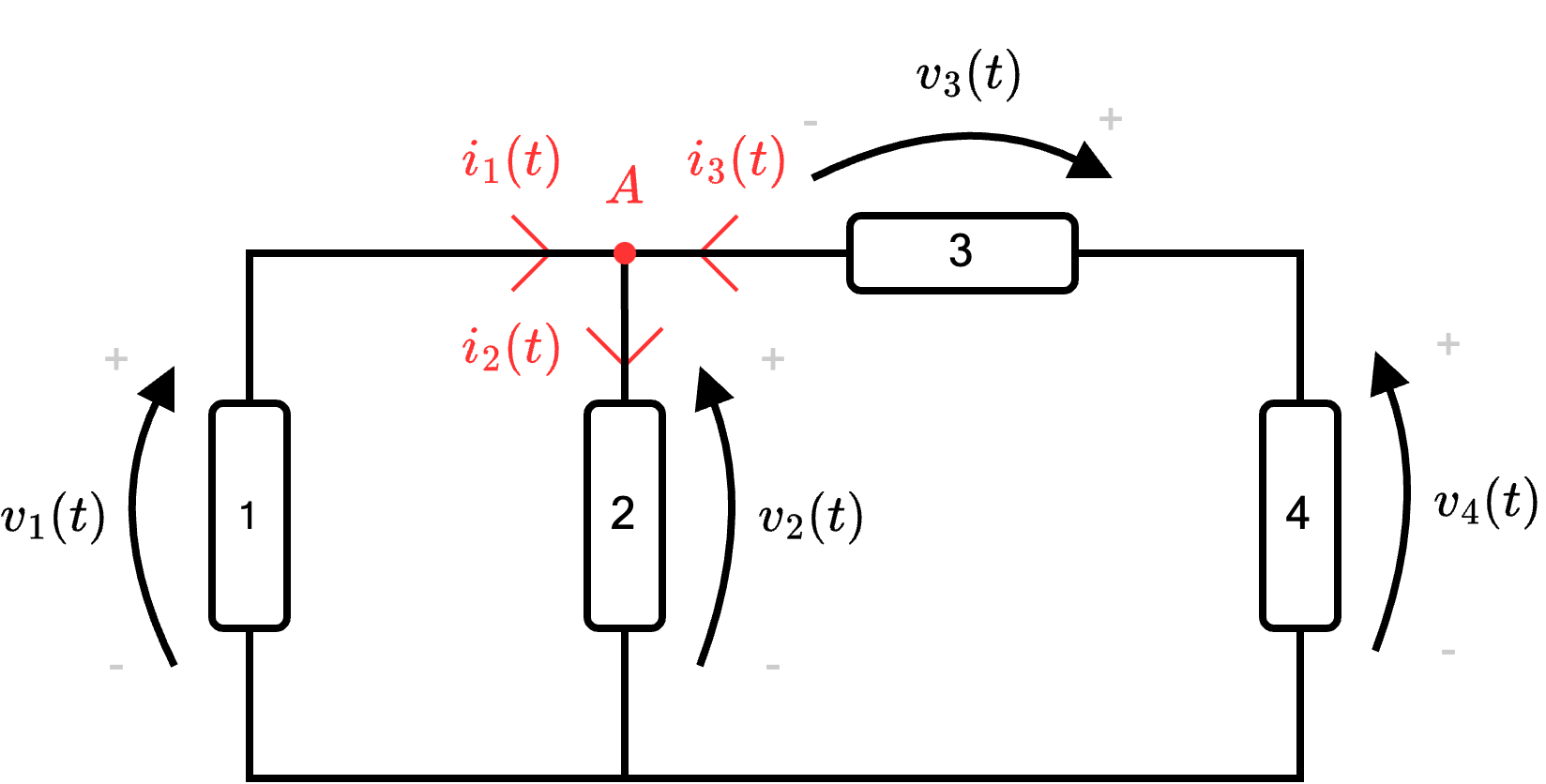
è possibile orientarlo e ottenere il seguente circuito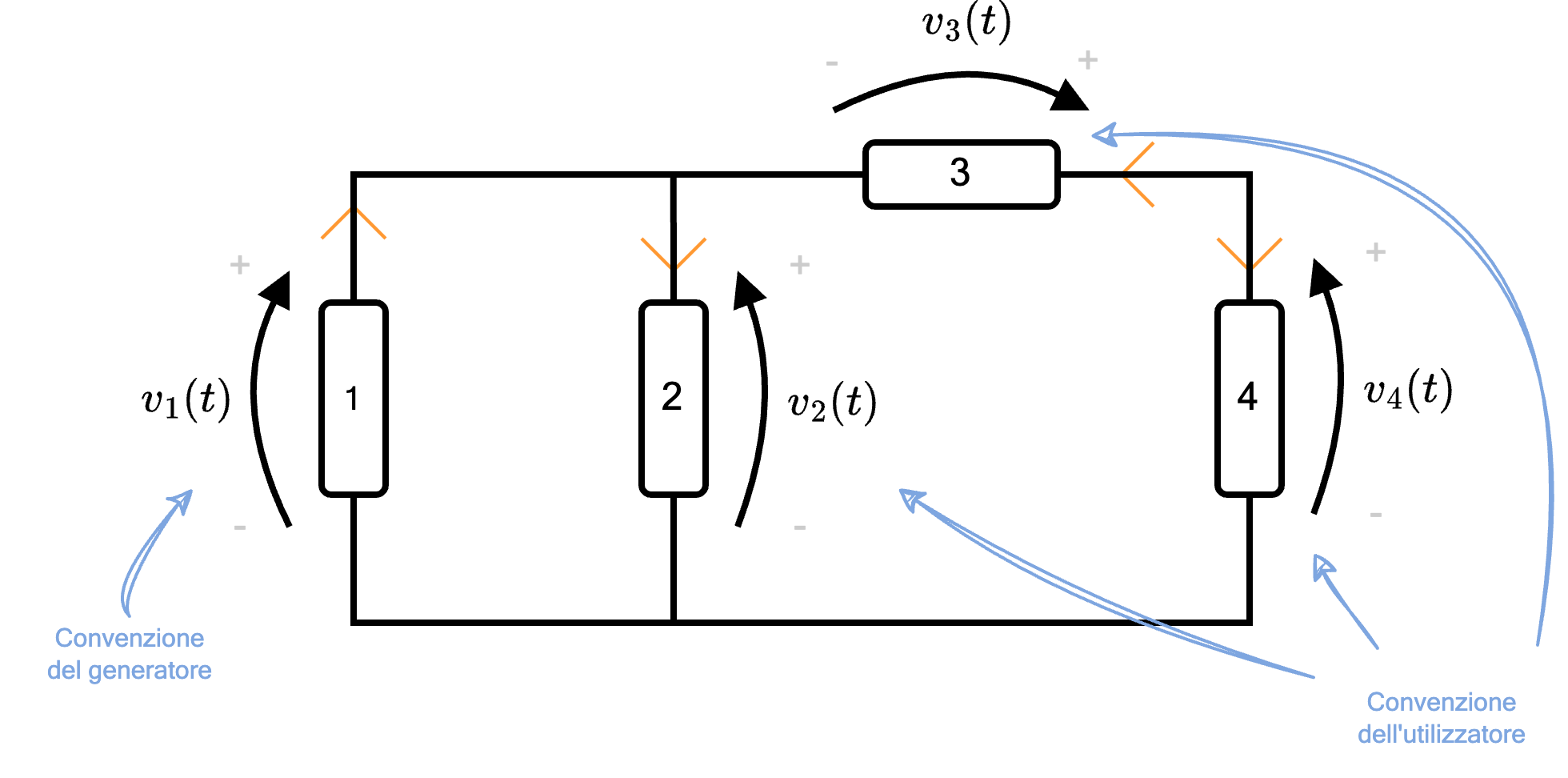 
Per determinare le equazioni delle correnti, è necessario identificare i nodi presenti:
- consideriamo il nodo \( A\) e assegnando segno positivo alle correnti "che entrano" e segno negativo a quelle "che escono", si ottiene l'equazione \[ A \quad : \qquad i_1 - i_2 + i_3 = 0 \]
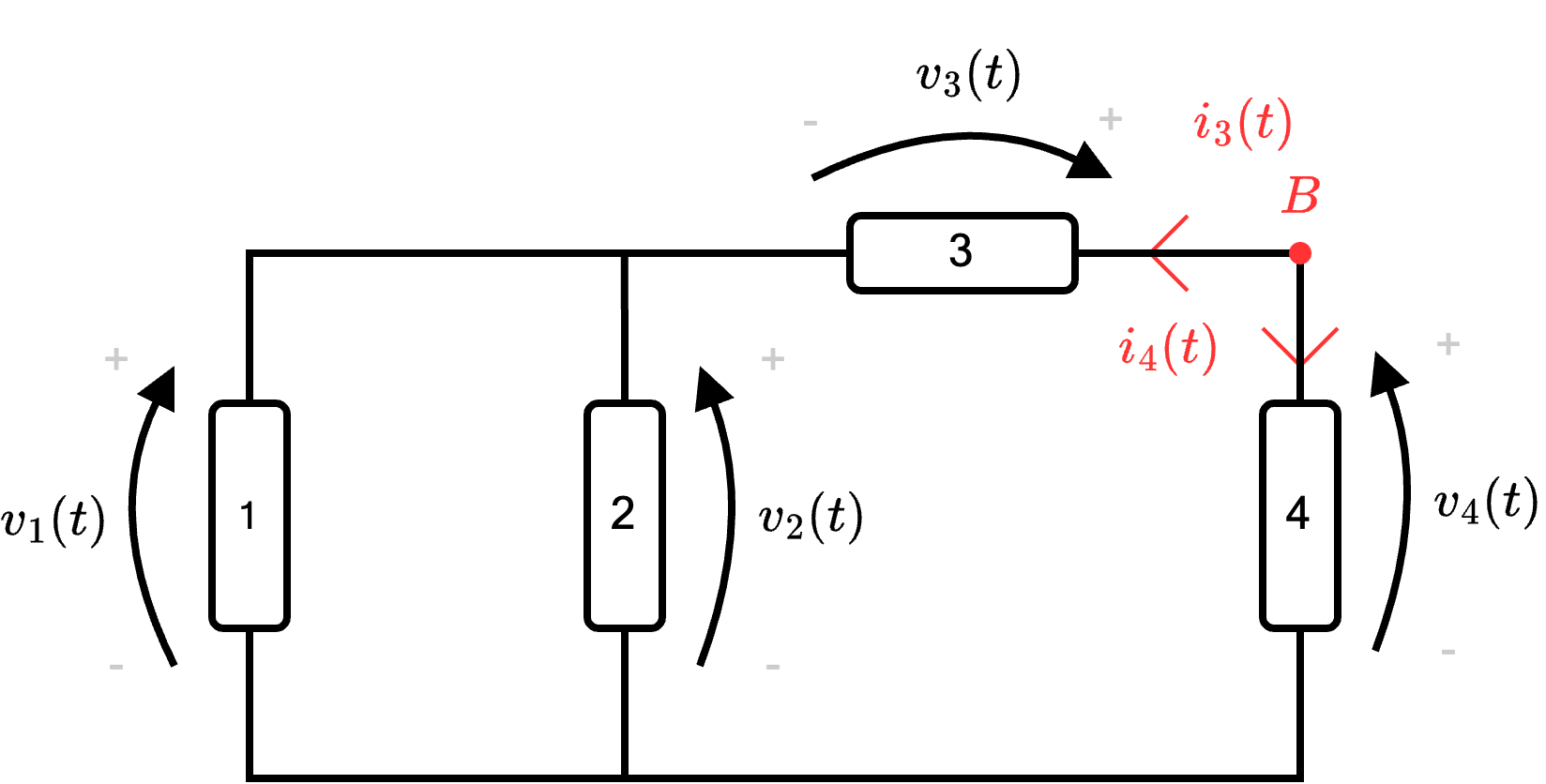
- consideriamo il nodo \( B\) e otteniamo l'equazione \[ B \quad : \qquad -i_3 - i_4 = 0 \]
- consideriamo il nodo \( C\) e otteniamo l'equazione \[ C \quad : \qquad -i_1 + i_2 + i_4 = 0 \]
